이진 탐색 트리 (Binary Search Tree)

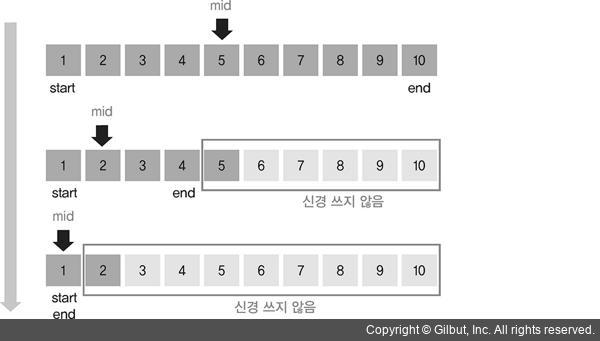
이진 탐색 알고리즘

• 정렬된 데이터로 된 리스트(배열이나 연결 리스트)가 인수로 들어왔을 때, 요소 중에 찾고자 하는 데이터가 있는지 알아보는 알고리즘

딕셔너리의 내부 구현

• 딕셔너리는 <key, item>의 쌍으로 된 집합
• 내부적으로 BST, 해시 테이블 두 가지 자료 구조로 구현 가능
• C++의 map은 BST의 변형인 균형 이진 트리, 그 중에서도 레드 블랙 트리를 이용해서 구현
• 자바에서는 HashMap과 TreeMap을 모두 유저 프로그래머가 내부 구현을 선택할 수 있도록 함
• 자바는 레드 블랙 트리를 사용하여 구현함

이진 탐색 트리

• 검색 효율을 높이기 위해 만든 이진 트리
• 노드에 데이터를 직접 저장하지 않는다
• 데이터에 대한 참조만 저장
• 데이터의 참조를 저장하고 있는 노드를 나타내는 키가 중요
• 키만 빠르게 검색 할 수 있다면 데이터는 참조를 이용해서 바로 접근 할 수 있다
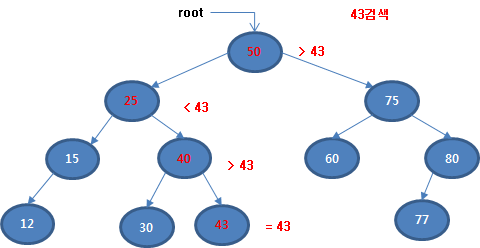
• 이진 탐색 트리의 정의
  1. 모든 키는 유일합니다.
  2. 어떤 노드를 특정했을 때 이 노드의 키 값은 왼쪽 서브 트리의 그 어떤 키보다 큽니다.
  3. 어떤 노드를 특정했을 때 이 노드의 키 값은 오른쪽 서브 트리의 그 어떤 키 값보다 작습니다.
  4. (재귀적 정의) 노드의 서브 트리도 이진 탐색 트리입니다.

  

이진 탐색 트리의 구현

class TreeNode:
    def __init__(self, key):
        self.__key=key
        self.__left=None
        self.__right=None
        self.__parent=None

    def __del__(self):
        print('key {} is deleted'.format(self.__key))

    @property
    def key(self):
        return self.__key

    @key.setter
    def key(self, key):
        self.__key=key

    @property
    def left(self):
        return self.__left

    @left.setter
    def left(self, left):
        self.__left=left

    @property
    def right(self):
        return self.__right

    @right.setter
    def right(self, right):
        self.__right=right

    @property
    def parent(self):
        return self.__parent

    @parent.setter
    def parent(self, p):
        self.__parent=p


class BST:
    def __init__(self):
        self.root=None

    def get_root(self):
        return self.root

    def preorder_traverse(self, cur, func):
        if not cur:
            return

        func(cur)
        self.preorder_traverse(cur.left, func)
        self.preorder_traverse(cur.right, func)

    # key가 정렬된 상태로 출력
    def inorder_traverse(self, cur, func):
        if not cur:
            return

        self.inorder_traverse(cur.left, func)
        func(cur)
        self.inorder_traverse(cur.right, func)

    # 편의 함수
    # cur의 왼쪽 자식을 left로 만든다.
    def __make_left(self, cur, left):
        cur.left=left
        if left:
            left.parent=cur

    # 편의 함수
    # cur의 오른쪽 자식을 right로 만든다.
    def __make_right(self, cur, right):
        cur.right=right
        if right:
            right.parent=cur

    def insert(self, key):
        new_node=TreeNode(key)

        cur=self.root
        if not cur:
            self.root=new_node
            return

        while True:
            parent=cur
            if key < cur.key:
                cur=cur.left
                if not cur:
                    self.__make_left(parent, new_node)
                    return
            else:
                cur=cur.right
                if not cur:
                    self.__make_right(parent, new_node)
                    return 

    def search(self, target):
        cur=self.root
        while cur:
            if cur.key==target:
                return cur
            elif cur.key > target:
                cur=cur.left
            elif cur.key < target:
                cur=cur.right
        return cur

    def __delete_recursion(self, cur, target):
        if not cur:
            return None
        elif target < cur.key:
            new_left=self.__delete_recursion(cur.left, target)
            self.__make_left(cur, new_left)
        elif target > cur.key:
            new_right=self.__delete_recursion(cur.right, target)
            self.__make_right(cur, new_right)
        else:
            if not cur.left and not cur.right:
                cur=None
            elif not cur.right:
                cur=cur.left
            elif not cur.left:
                cur=cur.right
            else:
                replace=cur.left
                replace=self.max(replace)
                cur.key, replace.key=replace.key, cur.key
                new_left=self.__delete_recursion(cur.left, replace.key)
                self.__make_left(cur, new_left)
        return cur

    def delete(self, target):
        new_root=self.__delete_recursion(self.root, target)
        self.root=new_root

    def min(self, cur):
        while cur.left != None:
            cur=cur.left
        return cur 

    def max(self, cur):
        while cur.right != None:
            cur=cur.right
        return cur

    def prev(self, cur):
        # 왼쪽 자식이 있다면
        # 왼쪽 자식에서 가장 큰 노드
        if cur.left:
            return self.max(cur.left)
        
        # 부모 노드를 받아온다
        parent = cur.parent
        # 현재 노드가 부모 노드의 왼쪽 자식이면 
        while parent and cur==parent.left:
            cur=parent
            parent=parent.parent
        
        return parent

    def next(self, cur):
        # 오른쪽 자식이 있다면
        # 오른쪽 자식에서 가장 작은 노드
        if cur.right:
            return self.min(cur.right)
        
        # 부모 노드를 받아온다
        parent = cur.parent
        # 현재 노드가 부모 노드의 오른쪽 자식이면
        # 루트에 도달하거나
        # 현재 노드가 부모 노드의 왼쪽 자식이 될 때까지
        # 계속 부모 노드로 이동
        while parent and cur==parent.right:
            cur=parent
            parent=parent.parent
        
        return parent      

if __name__=="__main__":
    print('*'*100)
    bst=BST()

    bst.insert(6)
    bst.insert(3)
    bst.insert(2)
    bst.insert(4)
    bst.insert(5)
    bst.insert(8)
    bst.insert(10)
    bst.insert(9)
    bst.insert(11)

    f=lambda x: print(x.key, end='  ')

    #bst.preorder_traverse(bst.get_root(), f)
    bst.inorder_traverse(bst.get_root(), f)
    print()
    
    searched_node = bst.search(8)
    if searched_node:
        print(f'searched key : {searched_node.key}')
        
        prev_node = bst.prev(searched_node)
        if prev_node:
            print(f'prev key : {prev_node.key}')
        else:
            print(f'this is the first key of the BST')

        next_node = bst.next(searched_node)
        if next_node:
            print(f'next key : {next_node.key}')
        else:
            print(f'this is the last key of the BST')
    else:
        print('there is no such key')
    print()


    print (f'MIN(bst) : {bst.min(bst.get_root()).key}')
    print(f'MAX(bst) : {bst.max(bst.get_root()).key}')

    #bst.delete(9)
    #bst.delete(8)
    bst.delete(6)

    #print(bst.delete(15))

    bst.preorder_traverse(bst.get_root(), f)
    # bst.inorder_traverse(bst.get_root(), f)
    print()
    print('*'*100)

이진 탐색 트리의 단점

• 정렬된 데이터가 삽입되면 각 레벨마다 노드가 하나씩만 있는 편형 이진 트리가 됨
• 연결 리스트와 같음
• 삽입, 삭제, 탐색 모두 O(n)

=> 이를 보완한 이진 탐색 트리가 레드 블랙 트리가 포함되는 균형 이진 트리