그래프 용어 정리

• 그래프는 로봇이 최단경로를 계산해서 움직일 때나 내비게이션 경로를 안내할때, 지하철역을 어디에 건설해야 가장 효율적인지 계산하는 등 매우 폭넓게 사용
• 그래프는 정점(vertex)의 집합 V(G)와 에지(edge)의 집합 E(G)로 정의

\[G = (V, E)\]

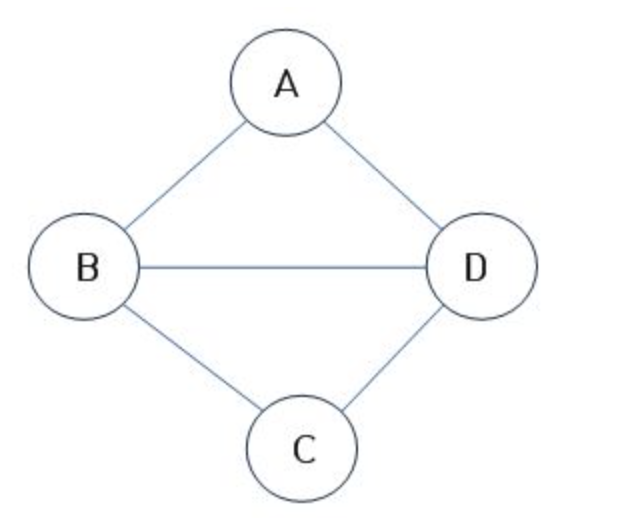
무방향 그래프

• 무방향그래프(undirected graph)인데, 이는 (A,B)은 (B,A)와 같다는 의미
• 정점 개수가 n개라면 이 그래프의 최대 에지 개수는 n * (n-1) /2

\[G = (V, E)\] \[V(G) = {A,B,C,D}\] \[E(G) = {(A,B),(A,D),(B,C),(B,D),(C,D)}\]

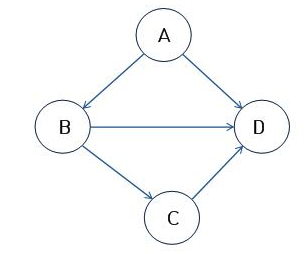
방향 그래프

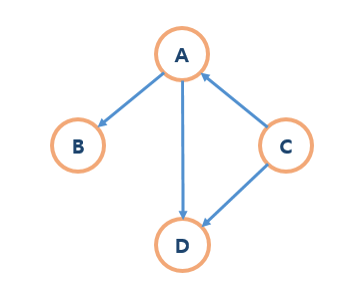
• 엣지에 방향이 있는 그래프

\[G = <V, E>\] \[V(G) = { A,B,C,D }\] \[E(G) = {<A,B><A,D>,<B,C>,<B,D>,<C,D>}\]

자기 간선

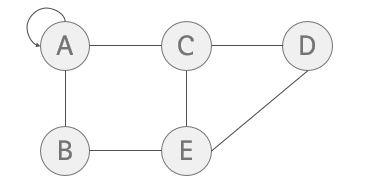
• 정점이 tail 이자 동시에 head 인 그래프

멀티그래프

• 일반적으로 그래프에서는 에지 중복 인정 하지 않는다.
• 이 중복 에지를 인정하는 자료 구조를 멀티 그래프(multi-graph)

인접

• 두 정점을 연결하는 간선이 있을 때 서로 인접한다고 표현

경로

• 경로란, 정점 Vi 에서 Vj까지의 정점 순서를 의미
• 경로길이는 에지 개수

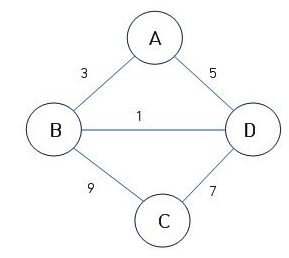
연결된 그래프

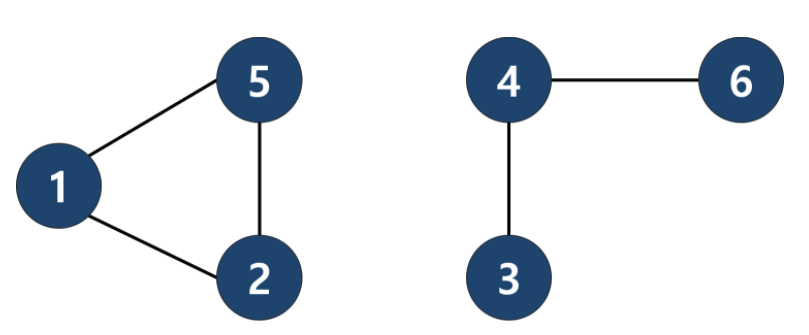
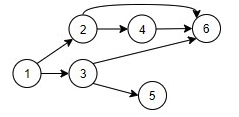
• 어떤 정점 u와 다른 어떤 임의의 정점 v를 골랐을 때 정점 사이에 경로가 있으면 이를 연결되었다 라고 한다.

\[G = (V, E)\] \[V(G) = {0,1,2,3,4,5,6}\] \[E(G) = {(1,2),(1,5),(2,5),(3,4),(4,6)}\]

• 정점 집합 {1,2,5},{3,4,6}을 각각 연결요소라고 한다.

차수

• 무방향 그래프의 경우 어떤 정점 v의 차수 d(v)는 정점 v가 부속된 에지 개수
• 무방향 그래프일 경우, 정점 A에 부속된 에지가 세개이므로 d(A) = 3
• 방향 그래프일 경우, 진입차수와 진출차수의 합
• 진입차수는 정점 v로 들어오는 에지 개수
• 진출차수는 정점 v에서 나가는 에지 개수

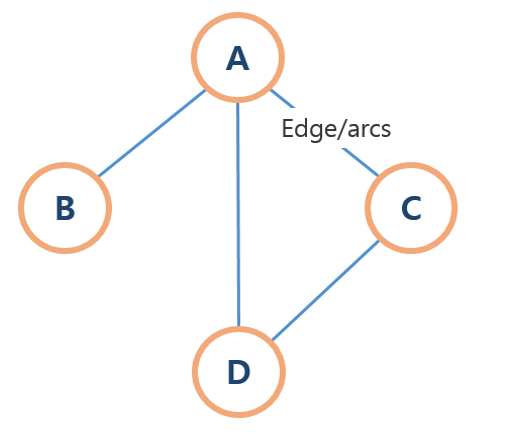
• 부속 : 정점 u와 정점 v 사이에 에지 (u,v)가 존재할 때 에지 (u,v)를 정점 u에 부속되었다라고 표현

그래프를 표현하는 두가지 방법: 도시와 도시를 이어보자

• 그래프를 표현 하는 두가지 방법에 인접 리스트(adjacency list) 와 인접행렬(adjacemcy matrix)이 있다.

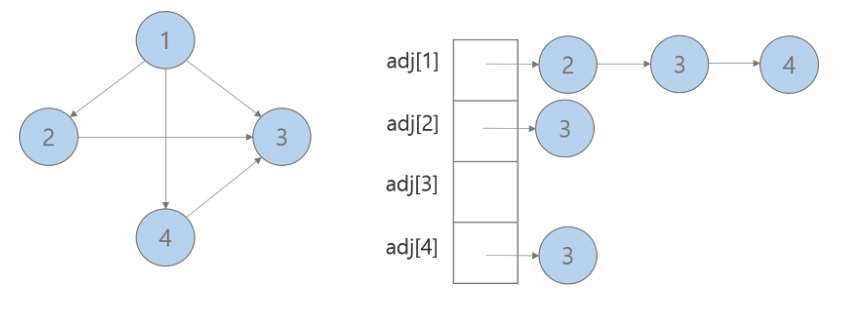
• 배열 한개와 연결리스트들로 구성되어있으며, 정점이 배열의 인덱스가 된다.
• 어떤 정점 v에 대해 인접한 모든 노드를 탐색하는 연산에 대한 빅오를 생각해보자
  • 정답 : 모든 정점을 조사할 필요 없이 해당 정점의 인접한 정점들만 조사하면되기 때문에 –> 빅오 O(d(v))

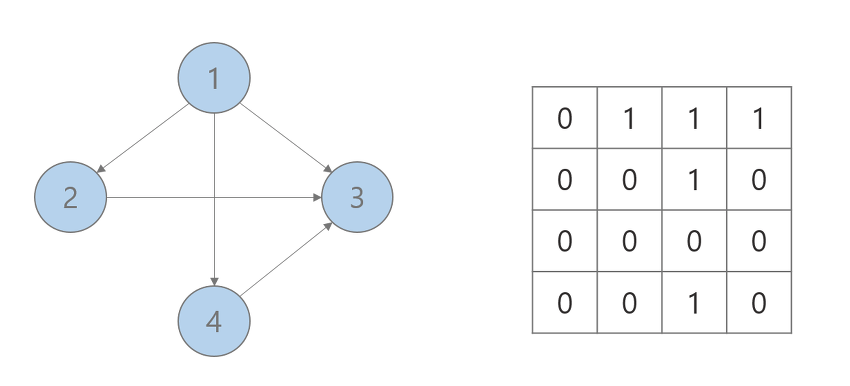
• 각각의 행을 정점으로 보고 열을 자신을 포함한 다른 정점이라고 생각하면 된다.
• matrix[1][3]의 값은 무엇일까요?
  • 정답 : 1
• 정점 n 에 대해 인접한 모든 노드를 탐색하는 연산에 대한 빅오를 생각해보자
  • 정답: 정점 개수가 n 이라고 했을때 O(n)
• (2,3)가 있는지 여부를 확인하는 연산에 대한 빅오를 생각해보자
  • 정답 : matrix[2][3]만 확인하면 되기 때문에 –> O(1)

그래프의 모든 노드 방문: 모든 도시를 여행해보자

• 모든 노드를 순회하는 방법은 두가지 : 너비 우선 탐색(Breadth Frist Search, BFS)과 깊이 우선 탐색 (Depth First Search, DFS)
• 너비 우선 탐색은 큐를 이용해서 구현, 깊이 우선 탐색은 스택을 기반으로 구현됩니다.

너비 우선 탐색(Breadth Frist Search, BFS) : 탐색을 할때 너비를 우선으로 하여 탐색을 수행하는 탐색 알고리즘

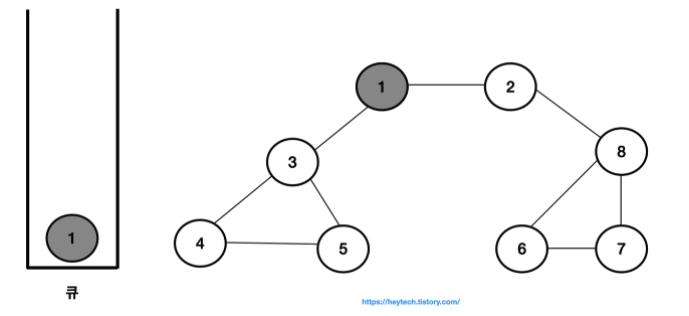
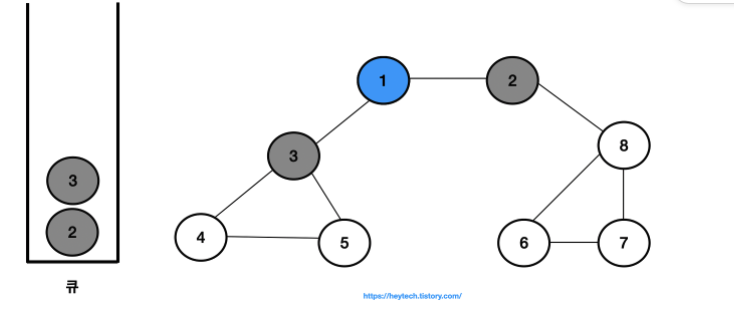
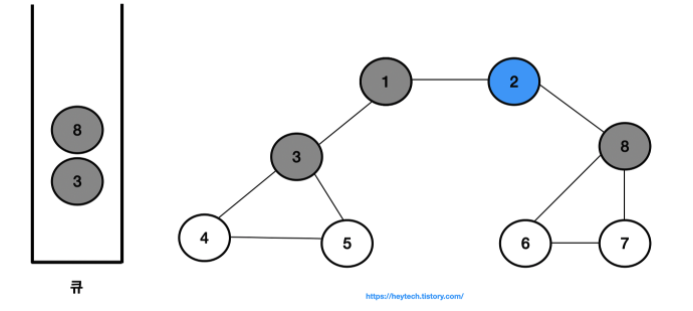
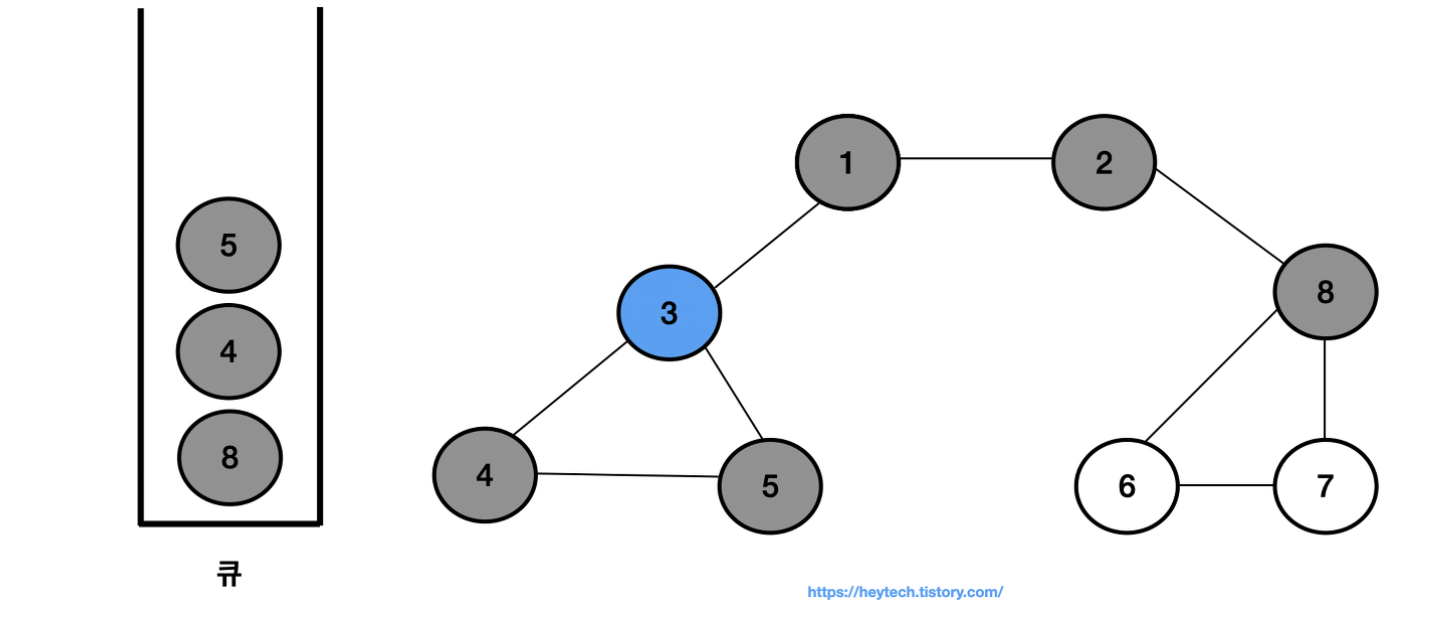
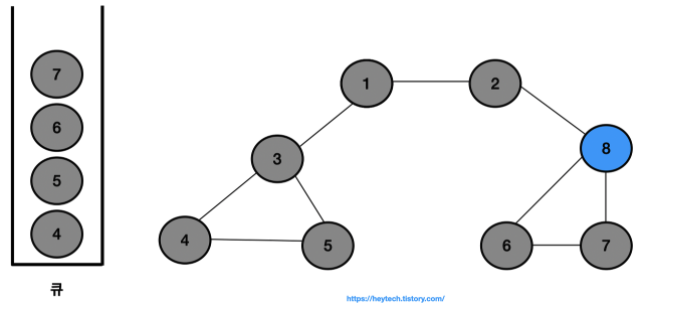
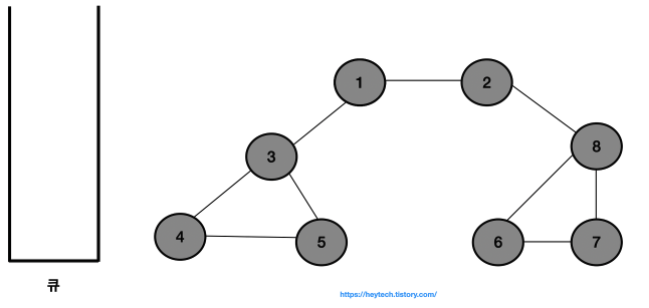
• 결과적으로 노드의 탐색 순서, 즉 큐에 삽입한 순서는 다음과 같습니다.
  • 1 -> 2 -> 3 -> 8 -> 4 -> 5 -> 6 -> 7

from queue import Queue

class Graph:
	def __init__(self, vertex_num):
        # 인접 리스트로 구현
		self.adf_list = [ [] for _ in range(vertex_num)]
        # 방문 여부 체크
		self.visited = [ False for _ in arnage(vertex_num)]
	
    def add_edge(self, u, v):
        self.adj_list[u].append(v)
        self.adj_list[v].append(u)

    def init_visited(self):
        for i in range(len(self.visited)):
            self.visited[i].False   

def bfs(self, v):
    q = Queue()
    # 방문 체크 리스트를 초기화합니다.
    self.init_visited()

    # 첫번째 정점을 큐에 넣고 방문 체크
    q.put(v)
    self.visited[v] = True

    while not q.empty():
        v = q.get()
        # 방문
        print(v, end=" ")
        # 인접 리스트를 얻어 옵니다.
        adj_v = self.adj_list[v]
        for u in adj_v:
            if not self.visited[u]:
                q.put(u)
                self.visited[u] = True

깊이 우선 탐색(Depth First Search, DFS) : 탐색을 할때 너비를 우선으로 하여 탐색을 수행하는 탐색 알고리즘

• 탐색을 할때 깊이를 우선으로 하여 탐색을 수행하는 탐색 알고리즘
• 한 노드를 시작으로 다음 노드로 넘어가기 전에 해당 노드를 완벽하게 탐색한다.

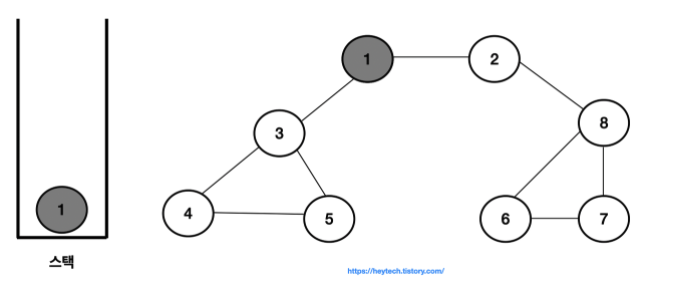
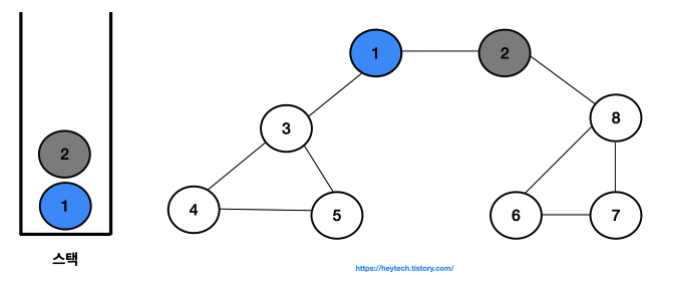
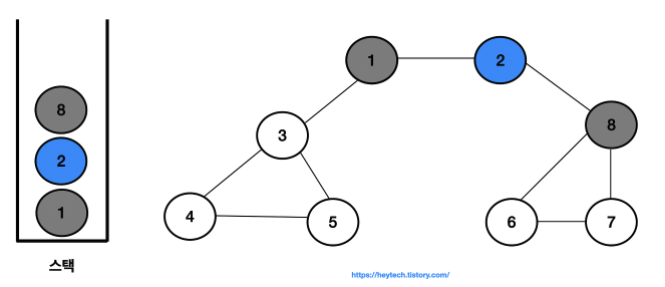
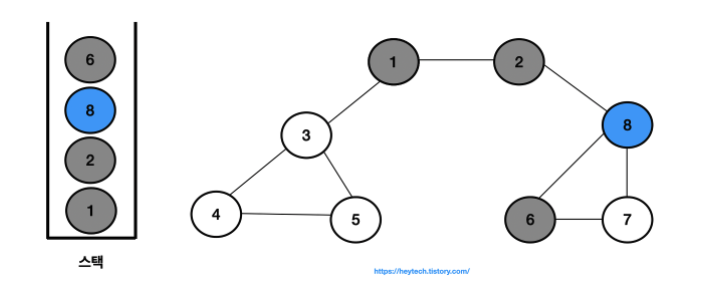
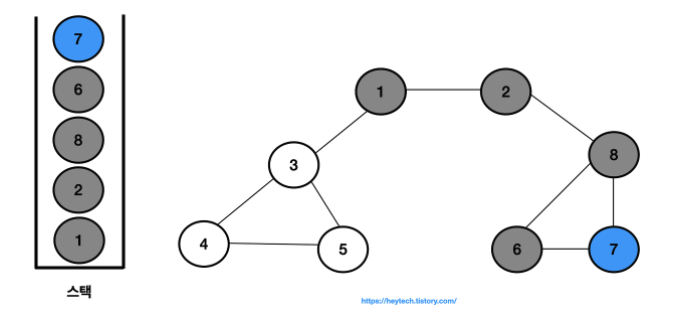
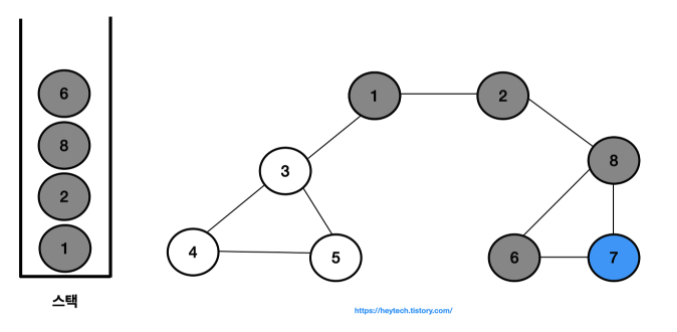
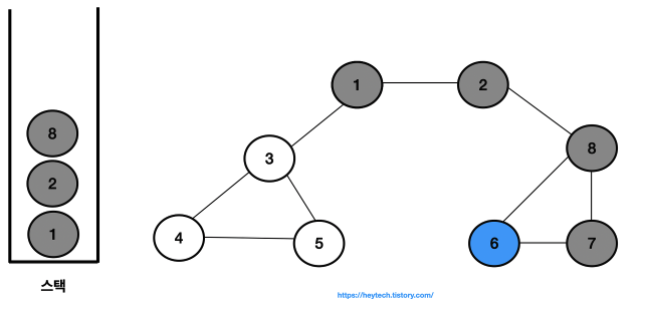
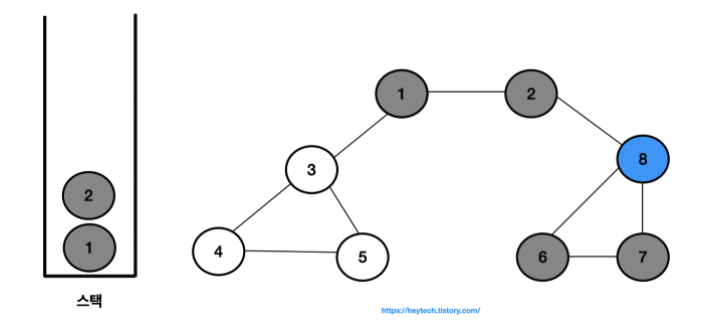
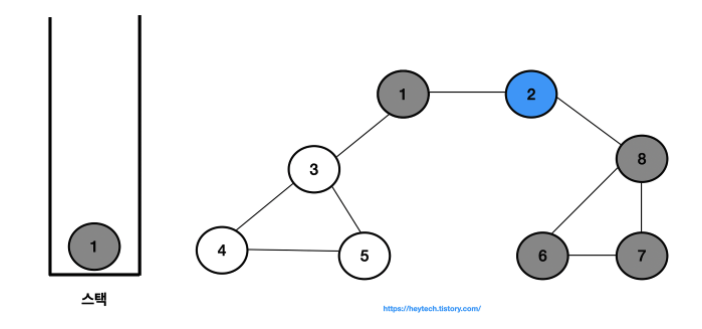
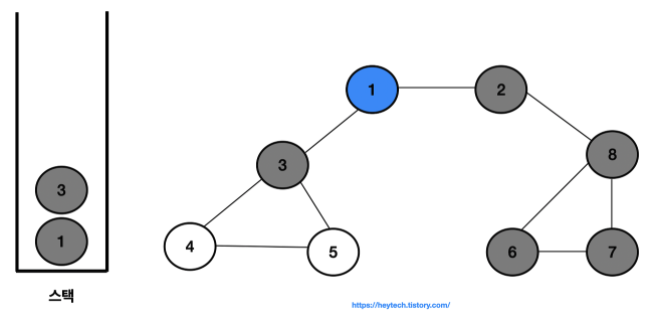
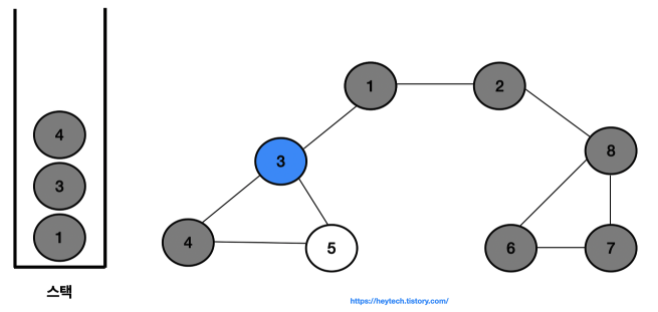
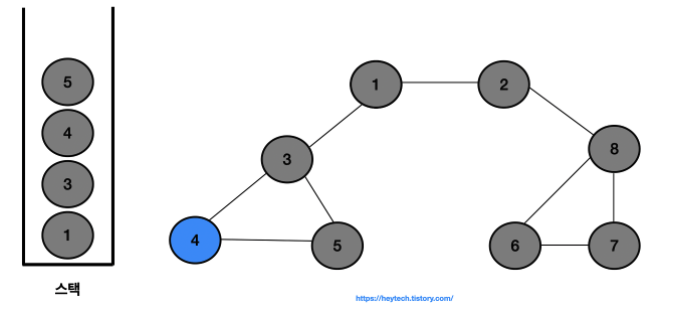
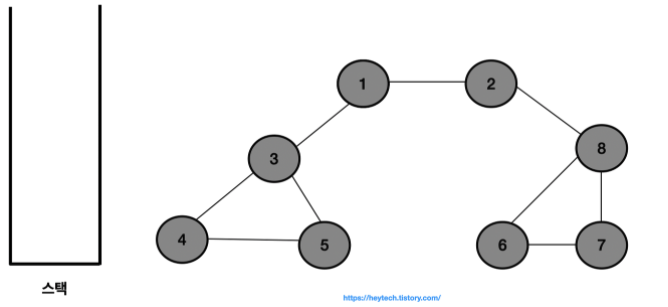
• 결과적으로 노드의 탐색 순서, 즉 스택에 삽입한 순서는 다음과 같습니다.
  • 1 -> 2 -> 8 -> 6 -> 7 -> 3 -> 4 -> 5

def dfs_recursion(self, v):
    # 방문
    print(v, end=" ")
    # 방문 체크
    self.visited[v] = True

    adj_v = self.adj_list[v]
    for u in adj_v:
        if not self.visited[u]:
            self.dfs_recursion(u)

def dfs(self,v):
    self.init_visited()
    self.dfs_recursion(v)

---

Source

https://heytech.tistory.com/55

https://heytech.tistory.com/56