Red Black Trees

Why are they used, and what rules do they follow?

Usage They allow to balance and optimize binary trees.

Rules

• Root node must be black
• Leaf nodes must be black
• Children of red nodes must be black
• All leaves have the same black depth

Quiz: Are those trees Red Black Trees?

None of them are Red Black Trees, they don’t respect all rules:

Insertion of new node

Inserting while keeping balance

When adding a node, the red-black balance must be kept. So there are operations to reequilibrate the tree:

• Rotation: interchange the position of nodes in a subtree. Left-Left position → Right Rotation:

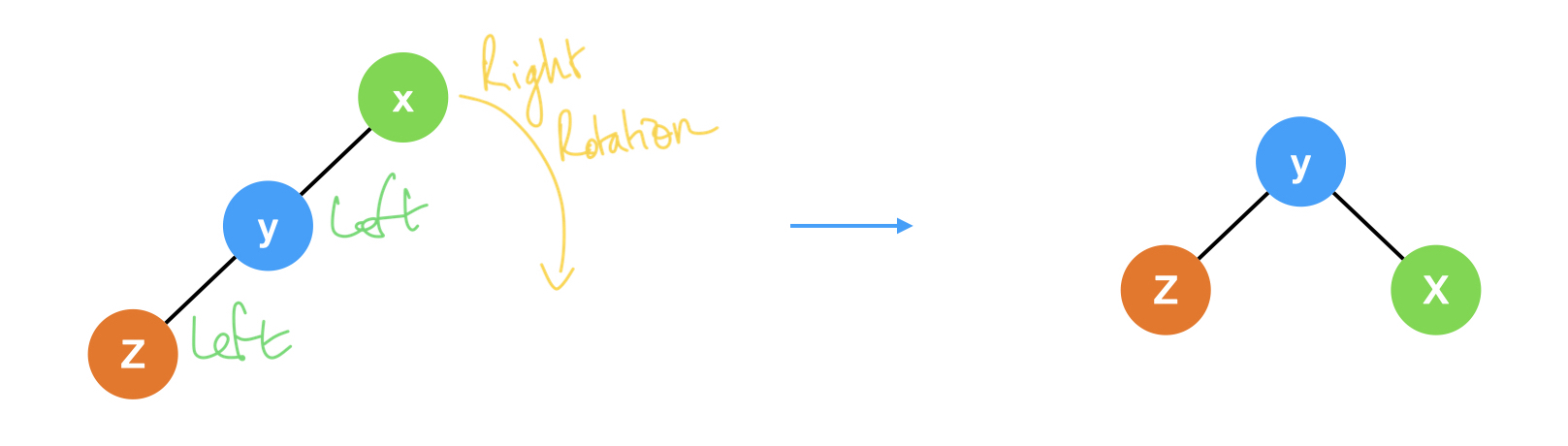
  Right-Right position → Left Rotation:

  

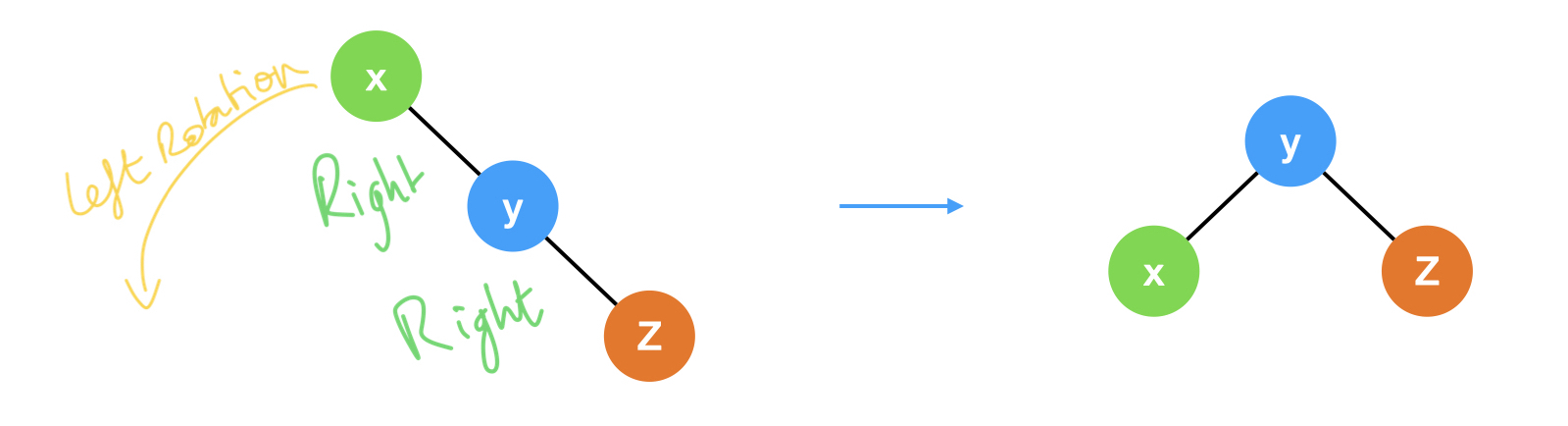
  Left-Right position → Right then Left rotation:

  

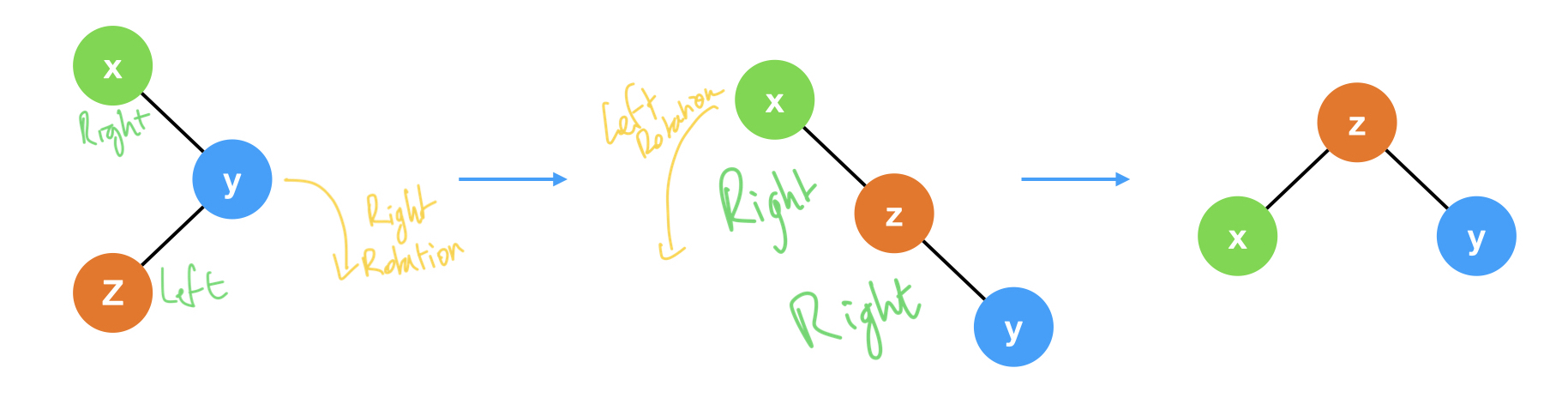
  Right-Left position → Left then Right rotation:

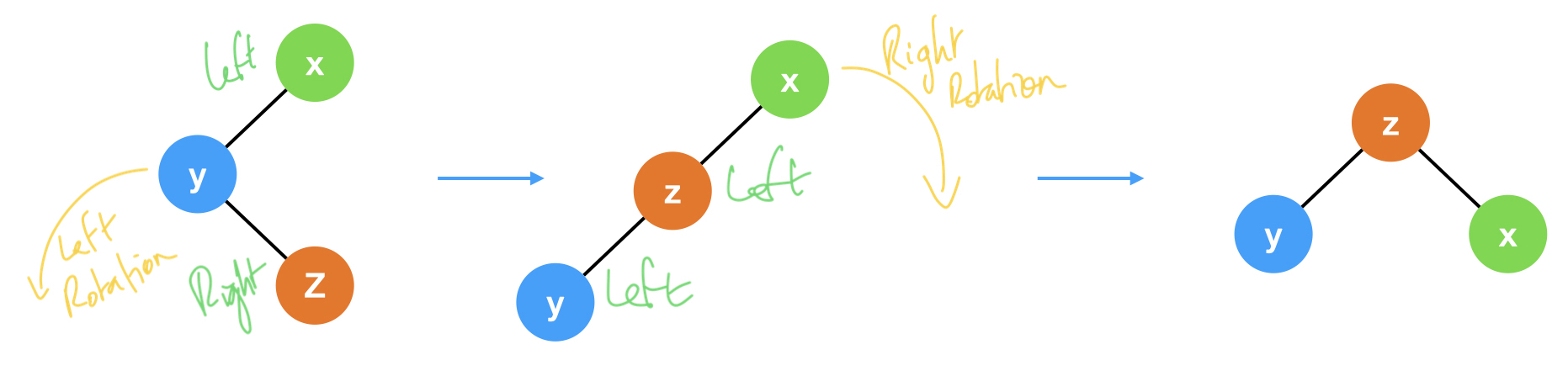
• Recoloring: update color to red or black

Algorithm

• [1] If tree is empty, first node (root node) is always black
• [2] If tree is not empty, new node is always red
• [3] If parent node is black - EXIT
• [4] If parent node is red - check uncle node
  • [4.a] If uncle is black or null: Rotation, and recolor
  • [4.b] If uncle is red: recolor, then check grandparent node:
    • [4.b.1] If grandparent is root EXIT
    • [4.b.2] If grandparent is not root, recolor and check Red-Black tree rules

Insertion exemple:

numbers to be inserted: 10 ; 18 ; 7 ;15 ; 16 ; 30 ; 25 ; 40 ; 60 ;2 ; 1 ; 70

Insert 10, 18, 7 and 15:

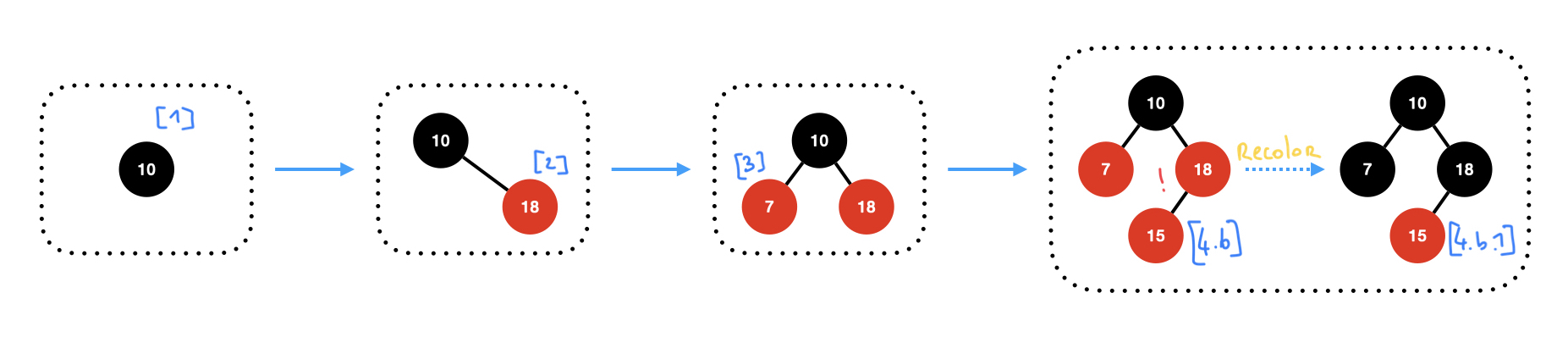
Insert 16 then 30:

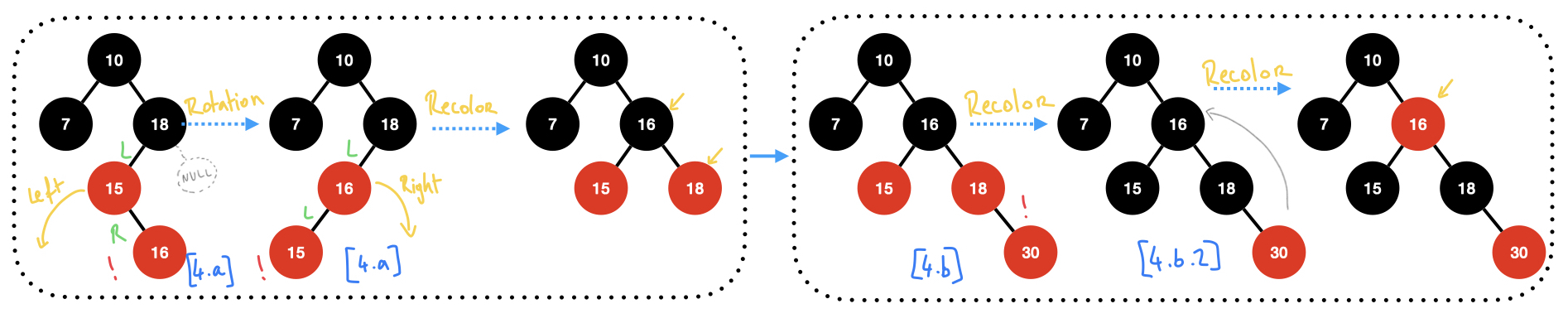
Insert 25:

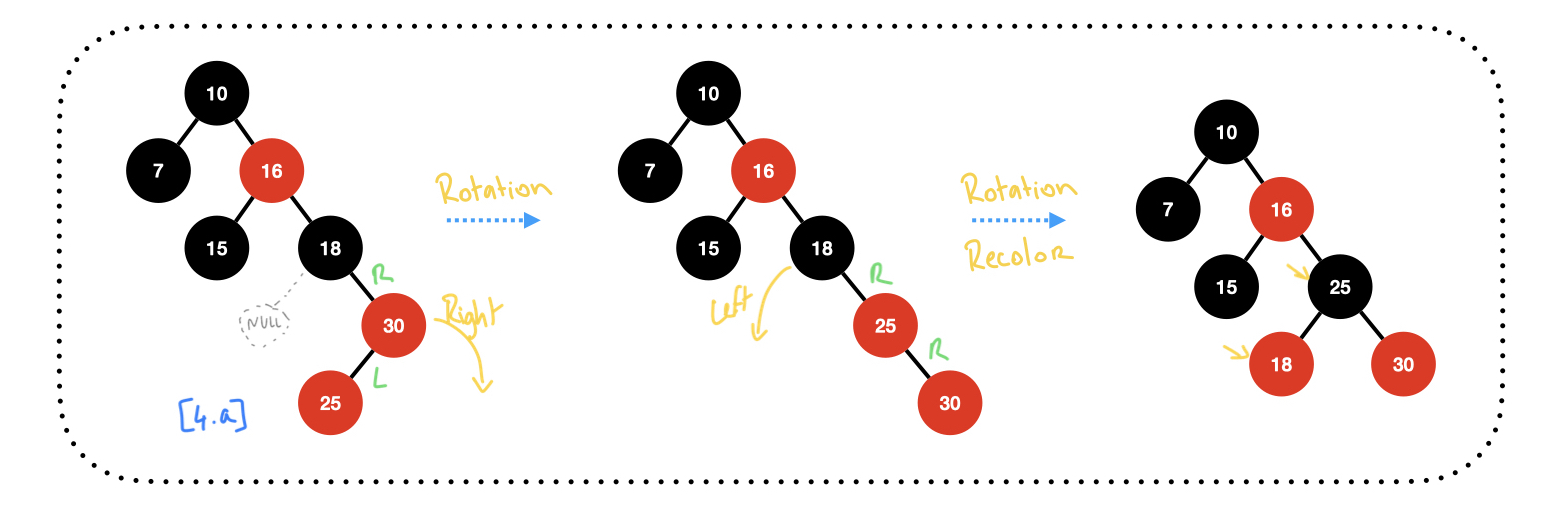
Insert 40:

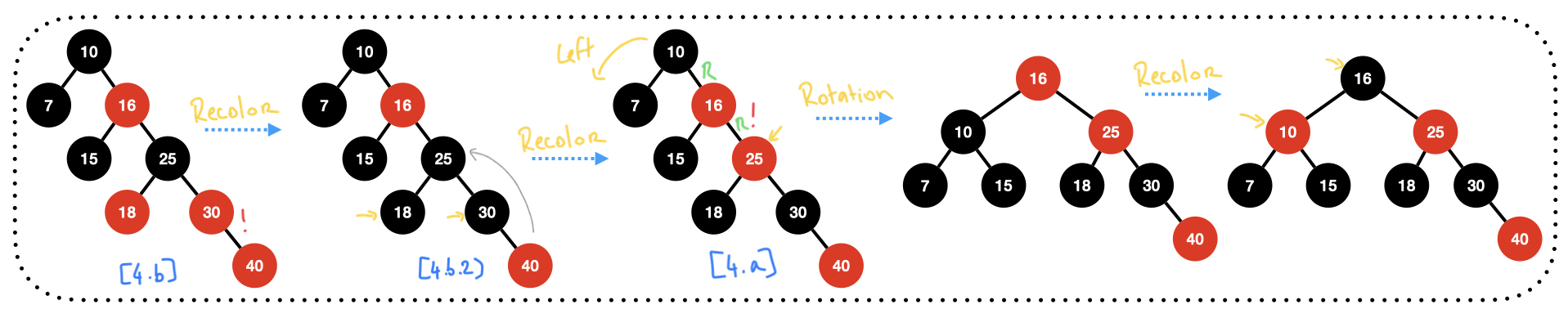
Insert 60 then 2:

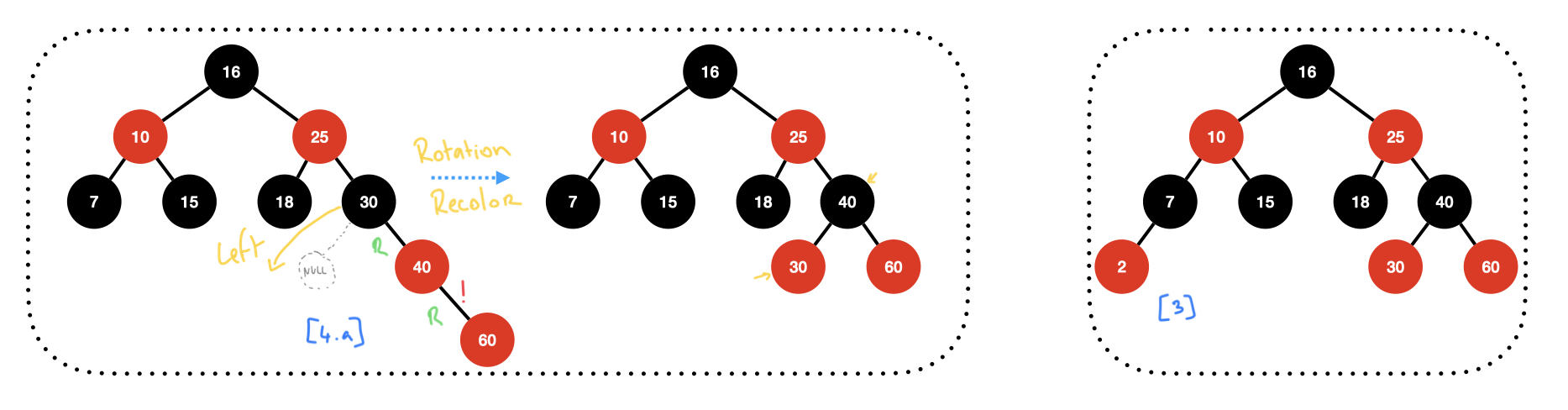
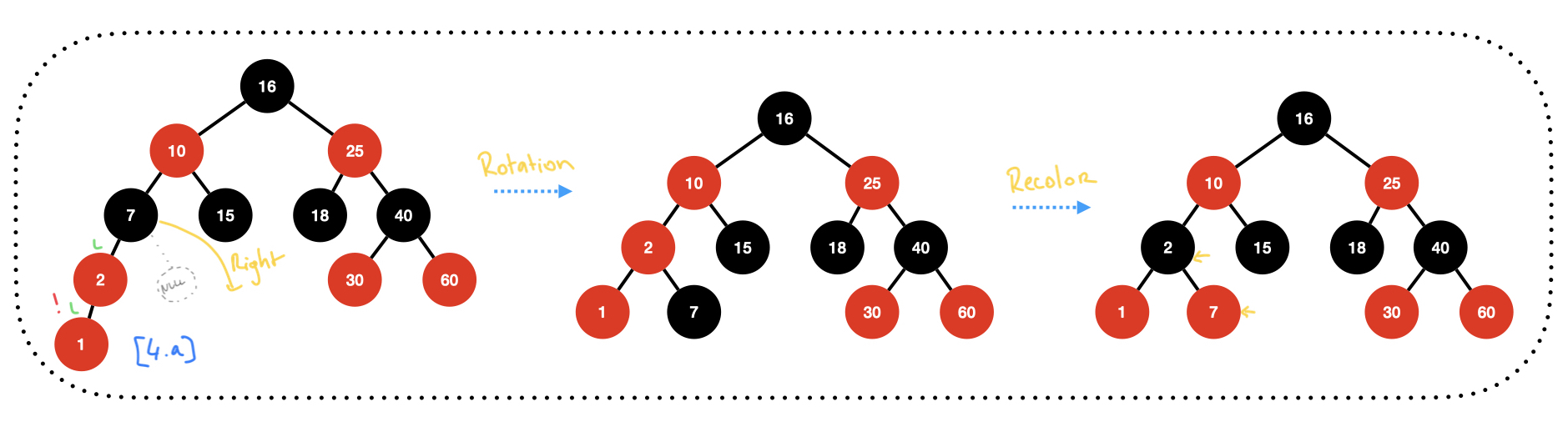
Insert 1:

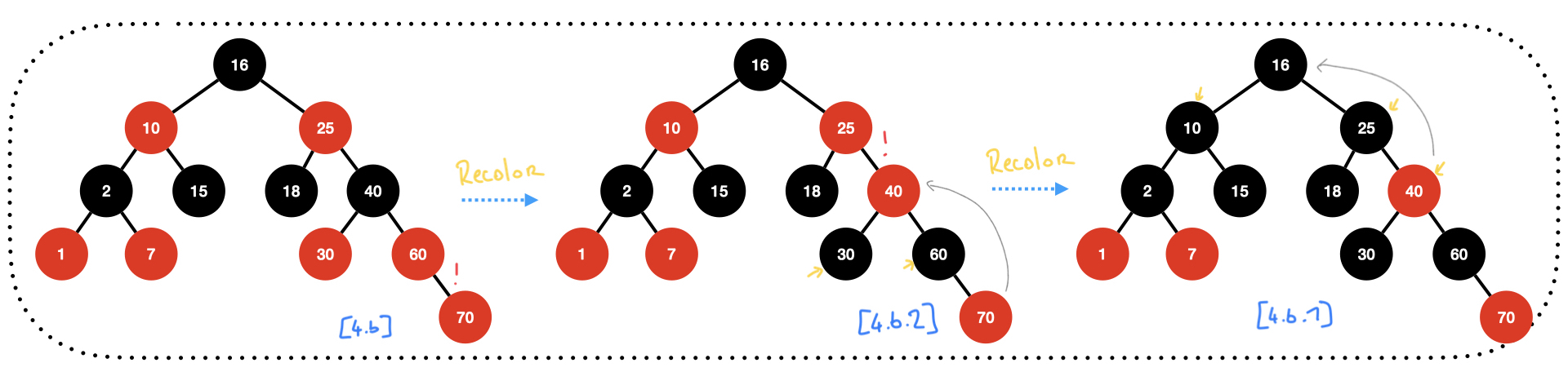
Insert 70:

Python code

## Red-Black node class:
class RBNode:
  def__init__(self, key):
    self.key = key #트리 내에서 유일한 키
    self.color = "RED" #노드색 - 연산할때 일단 RED로 함
    self.left = None
    self.right = None
    self.parent = None

  def __str__(self):
    return str(self.key)

## RedBlack Tree class +define ext node color as black
class RedBlackTree:
  def __init__(self):
    self.root__root = None
    self.__EXT = RBNode(None) #Each external nodes as one object
    self.__EXT.color = "BLACK" #External nodes are black
  
  def get_root(self):
    return self.__root
  
  def preorder_traverse(self,cur,func,*args,**kwargs):
    if cur == self.__EXT:
      return
    
    func(cur,*args,**kwargs)
    self.preorder_traverse(cur.left,func,*args,**kwargs)
    self.preorder_traverse(cur.right,func,*args,**kwargs)

## Left rotate - move nodes
def __left_rotate(self,n):
  r = n.right #n's right child
  l = r.left #r's left child
  
  #l becomes n's right child:
  l.parent = n 
  n.right = l
  
  #n.parent becomes r.parent
  #if n is root node, update the tree's root
  if m == self.__root:
    self.__root = r
    elif n.parent.left == n:
      n.parent.left = r
    else: 
      n.parent.right = r
      r.parent = n.parent
      
      #n becomes r's left child
      r.left = n
      n.parent = r

## Right rotate - move nodes
def __right_rotate(self,n):
  l = n.left #n's left child
  r = l.right #l's right child
  
  #r becomes n's left child
  r.parent = n
  n.left = r
  
  #n.parent becomes l.parent
  #if n is root node, update the tree's root
  if n == self.__root:
    self.__root = l
  elif n.parent.left == n:
    n.parent.left = l
  else:
    n.parent.right = l
  l.parent = n.parent
  
  #n becomes l's right child
  l.right = n
  n.parent = l

## Insert node rule - + add fix  
  def insert(self.key):
    new_node = RBNode(key)
    new_node.left = self.__EXT
    new_node.right = self.__EXT
    
    cur = self.__root
    if not cur:
      self.__root = new_node
      self.__root.color. = "BLACK" #root is always black
      return
    
    while True:
      parent = cur
      if key < cur.key:
        cur = cur.left
        if cur == self.__EXT:
          parent.left. = new_node
          new_node.parent = parent #set parent of node
          break
      else:
        cur = cur.right
        if cur == self.__EXT:
          parent.right = new_node
          new_node.parent = parent #set parent of node
          break
          
      self.__insert_fix(new_node) #after insertion, fix tree

      
## Fix algorithm
      
      def __insert_fix(self,n):
        pn = gn = un = None #pn is n's parent, gn is n's grandparent, un is n's uncle
        pn = n.parent
        
        while pn != None and pn.color == "RED": # n isn't root then if n.parent is RED then continuously red
          gn = pn parent #if pn is red, then n has grandparent. Root is BLACK so pn can't become root
          if gn.left == pn: #when pn is gn left's son
            un = gn.right
            
            if un.color == "RED": #when uncle is red
							#recolor grandparent, parent and uncle
              gn.color = "RED"
              pn.color = un.color = "BLACK" 
              
              n = gn #check grand parent for RDTree rules [4.b]
              pn = n.parent

            else: #when uncle is black
              if pn.right == n: #when LEFT-RIGHT and black uncle
                self.__left_rotate(pn)
                n, pn = pn,n
              pn.color, gn.color = gn.color, pn.color #recolor parent and grandparent
              
              self.__right_rotate(gn)
            else:
              un = gn.left # when grandparent left child is ext node, HELP???
              if un.color == "RED":
              	gn.color = "RED"
              	pn.color = un.color = "BLACK"
                
                n = gn
                pn = n.parent
              else:
                if pn.left == n:
                  self.__right_rotate(pn)
                  n,pn = pn,n
                  pn.color, gn.color = gn.color, pn.color
                  self.__left_rotate(gn)
         self.__root.color = "BLACK" #when red is continuous until root, change root to black.

    

Sources

What are **kwargs and *args

Red Black tree properties

Rotations explained

Red Black Tree node insertion

Red Black Tree node deletion