최소 비용 신장 트리 (Minimum Cost Spanning Tree)

• 사이클이 없는 연결된 그래프라면 이를 신장 트리(spanning tree)라고 한다.
• 최소 비용 신장트리 (Minimum Spanning Tree)는 가중치 무방향 그래프에서 모든 정점을 연결할 때 최소의 비용으로 연결할 수 있는 방법을 찾는 알고리즘이다.
• 최소비용신장 알고리즘에는 크루스칼 알고리즘과 프림 알고리즘이 존재한다.

탐욕 알고리즘(Greedy algorithm)

• 크루스칼 알고리즘이나 프림알고리즘 모두 탐욕 알고리즘의 한 종류
• 탐욕 알고리즘은 매 단계마다 항상 최적일 것 같은 선택을 하면 전체적으로도 최선의 선택을 하게 된다는 알고리즘이다.
• 즉, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
• 탐욕 알고리즘을 적용하려면 두가지 제약조건을 만족해야 사용할 수 있다. 이 두가지 제약 조건을 탐욕 특성(greedy properties)라고 한다.

최적 부분 구조(optional substructure) : 어떤 전체 문제에 대한 최적해는 부분문제에 대한 최적해를 포함하고 있다.

탐욕 선택 특성(greedy choice property) : 부분적으로 최적의 선택을 계속하면 전역적으로 최적해에 도달할 수 있습니다.

• 탐욕 선택 특성인 컷 프로퍼티(cut property)

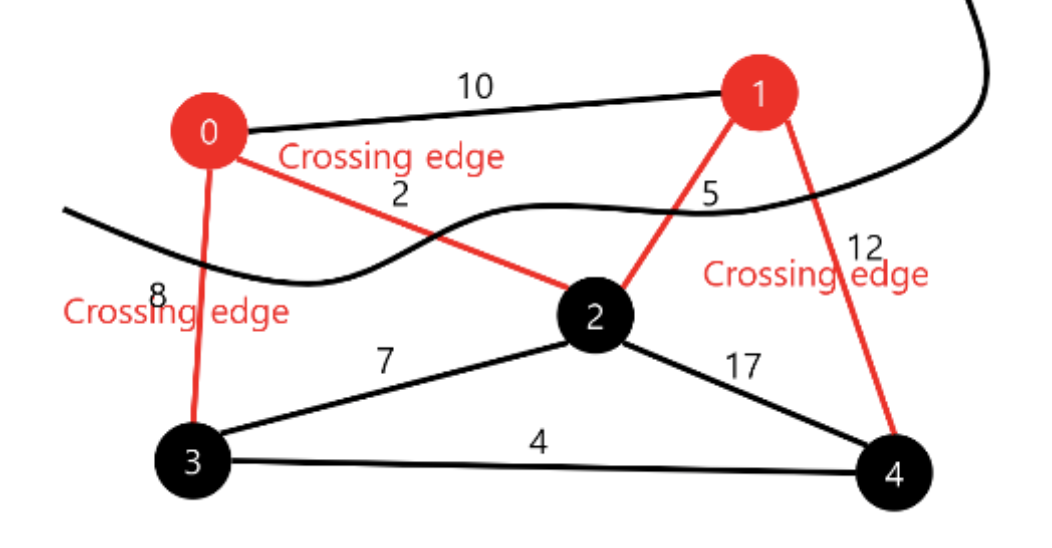
• V(G) 집합을 공집합이 아닌 두 집합으로 나눈 것
• Crossing edge : 컷으로 나뉜 한 집합의 정점과 다른 집합의 정점을 연결
• Cut property : Crossing edge 중 가장 작은 에지로, MST의 한 에지가 된다.
• Kruskal과 Prim 모두 Cut property 기반으로 만들어졌으며, 다른 점은 어떻게 자를 것인가의 차이이다.

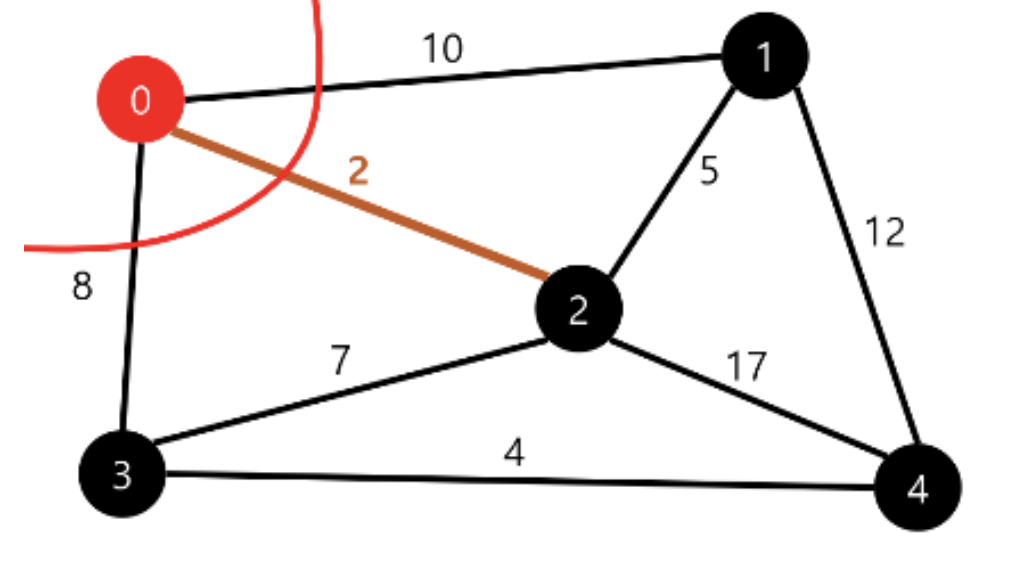
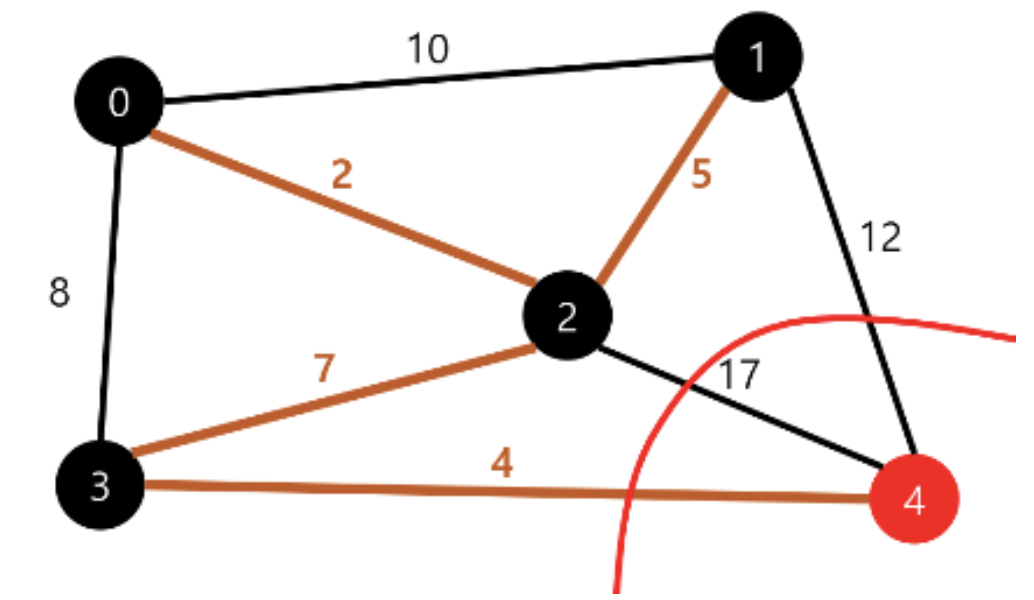
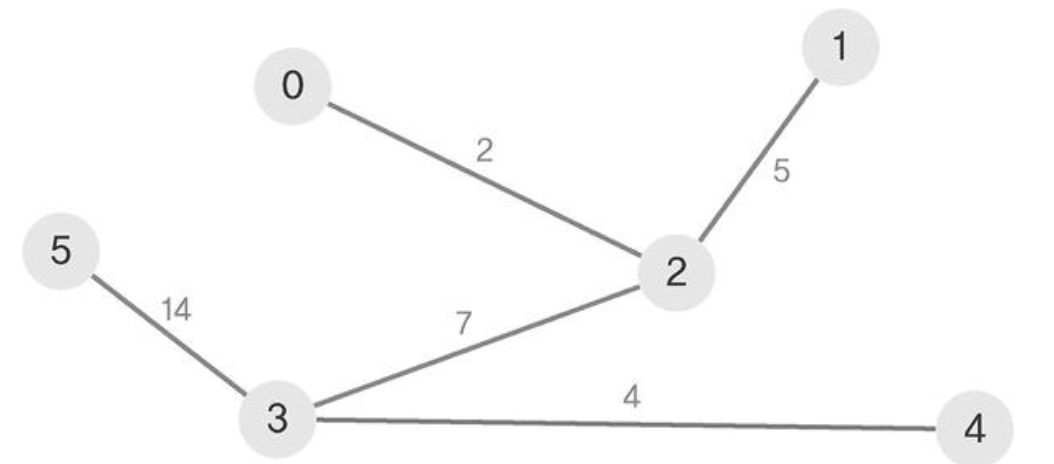
① 시작점에서 인접한 정점을 주변으로 컷을 찾는다. crossing edge 중에서 가중치가 가장 작은 에지인 2를 선택한다.

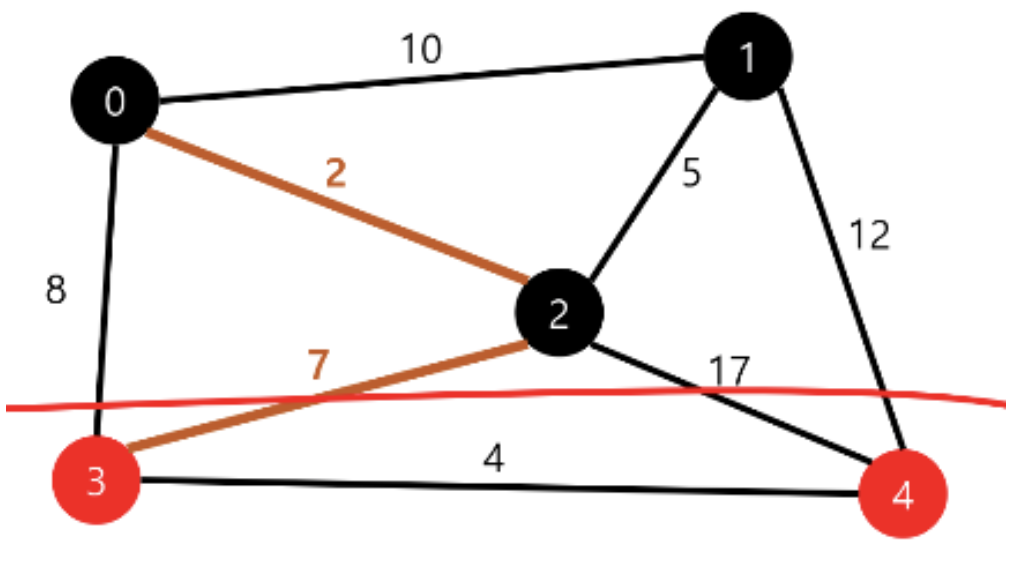
② crossing edge 중에서 가중치가 가장 작은 에지인 7을 선택한다. 선택된 crossing edge를 포함하지 않는 컷을 찾는다.

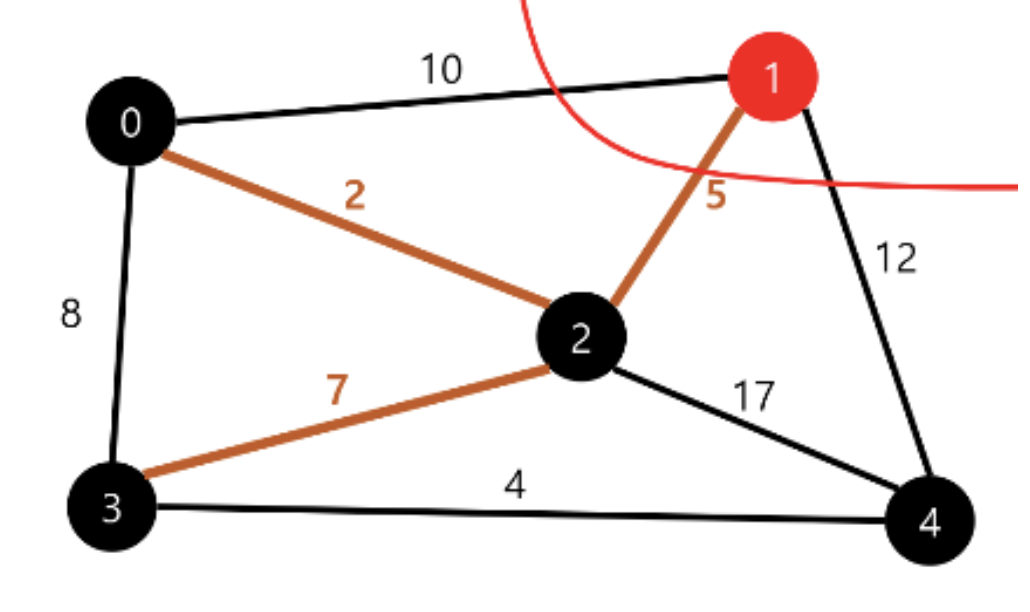
③ crossing edge 중에서 가중치가 가장 작은 에지인 5를 선택한다.

④ crossing edge 중에서 가중치가 가장 작은 에지인 4를 선택한다. ⑤

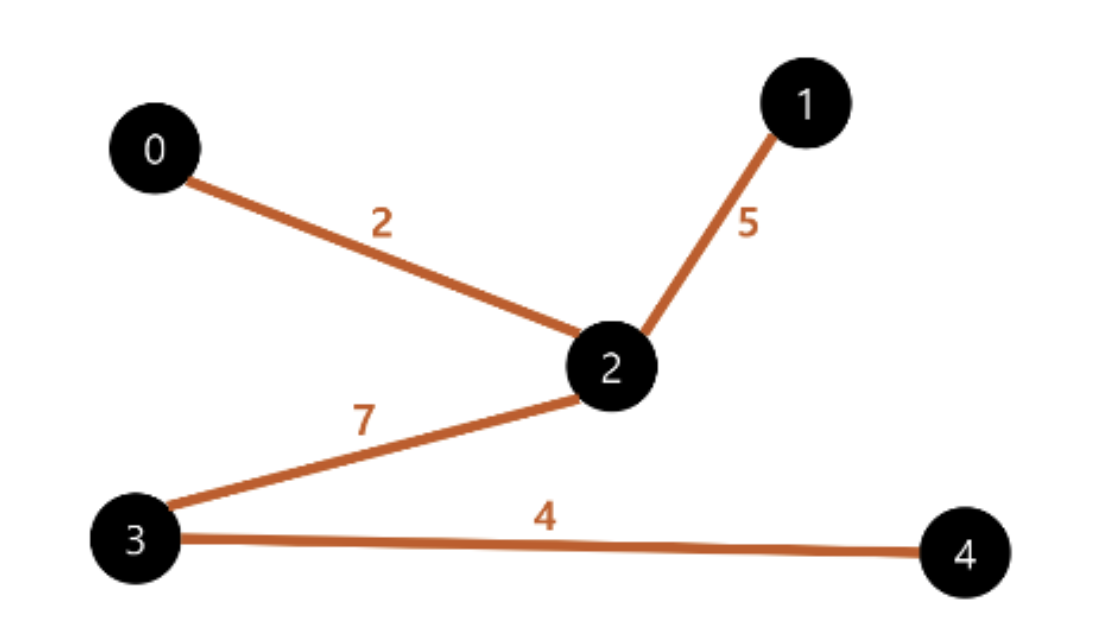
크루스칼 알고리즘(Kruskal algorithm)

• 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘
• 여러 개의 도시가 있을 때, 각 도시 사이를 연결하는 도로를 최소한의 비용으로 건설하고 할 때 적용되는 알고리즘

크루스칼 알고리즘 동작

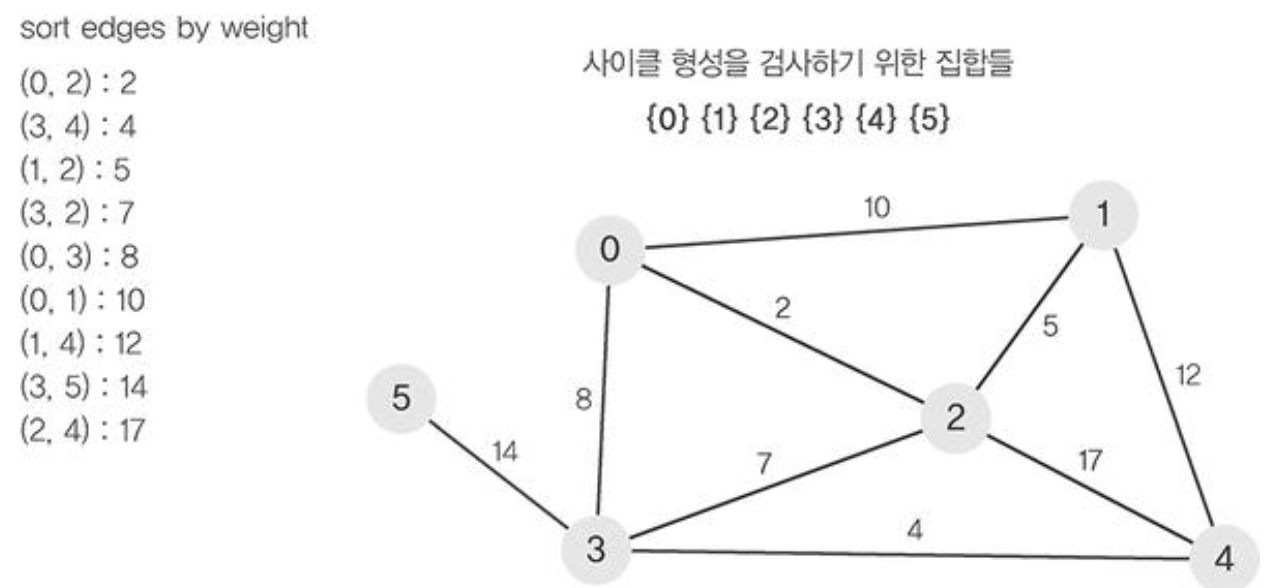
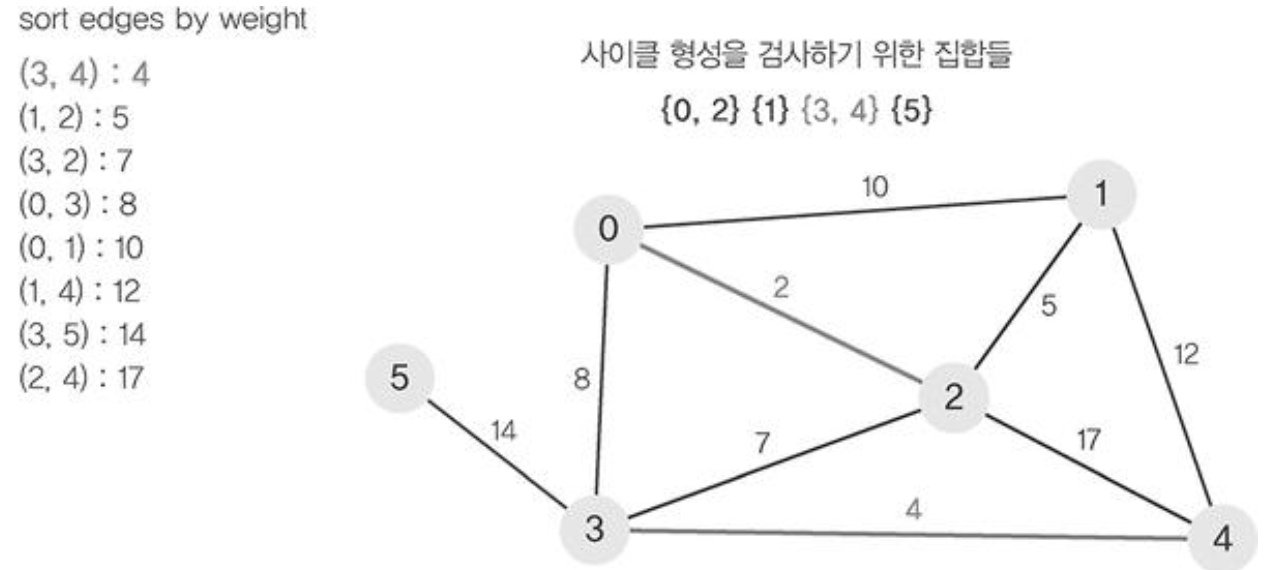
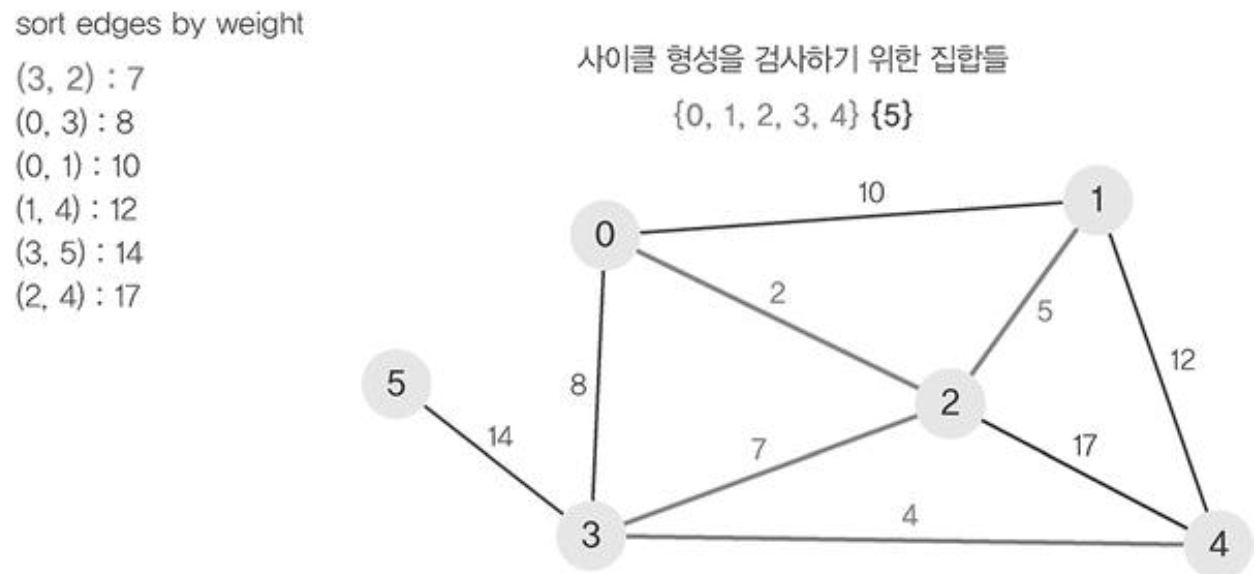
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
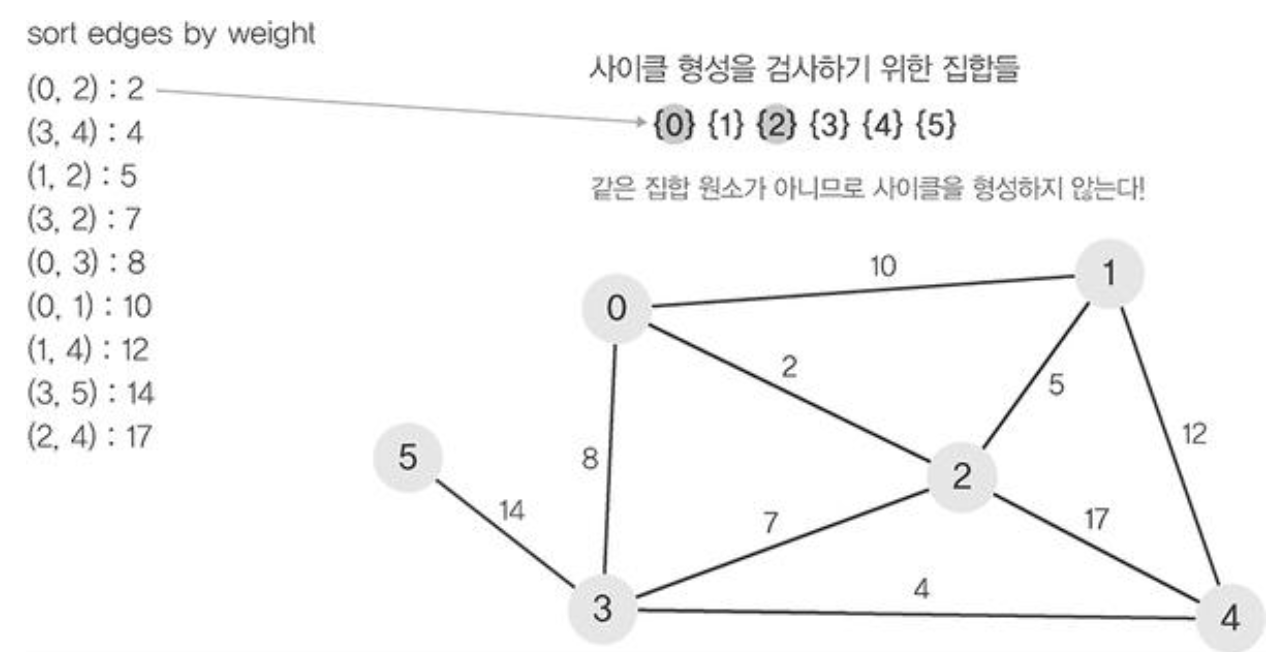
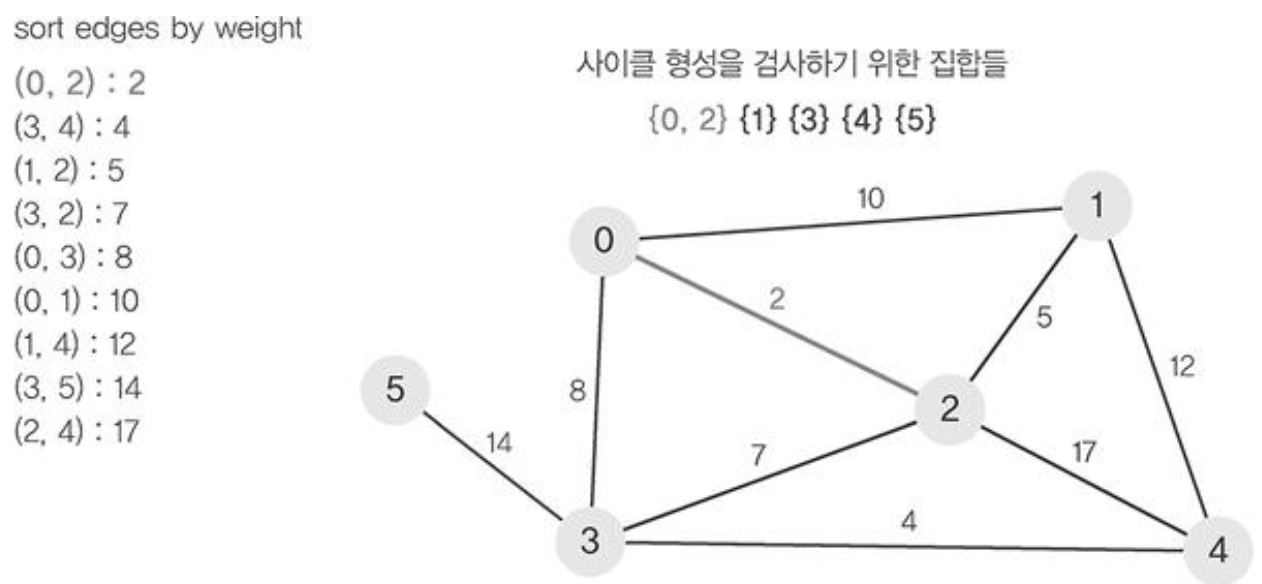
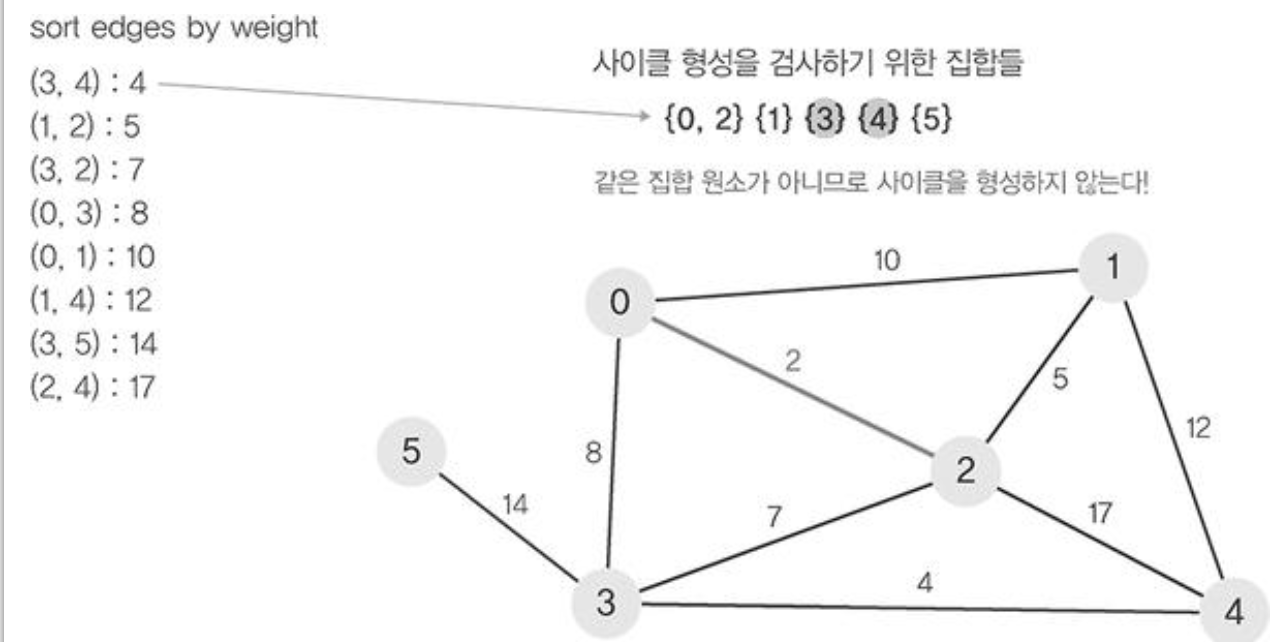
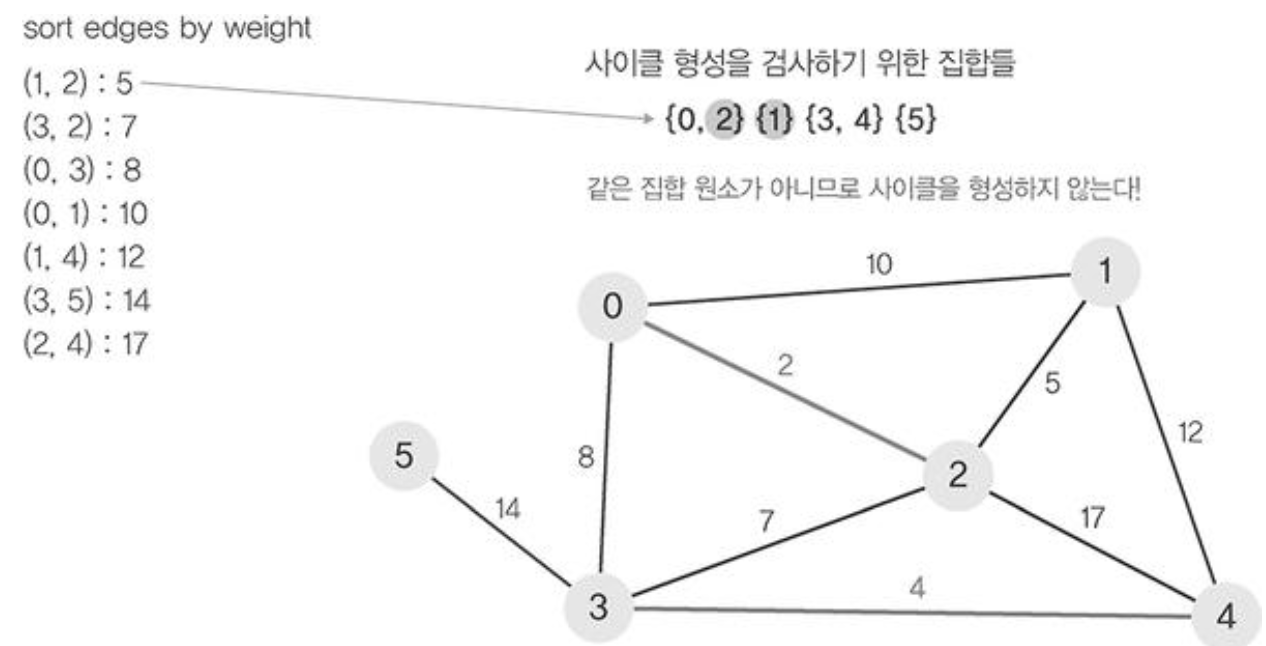
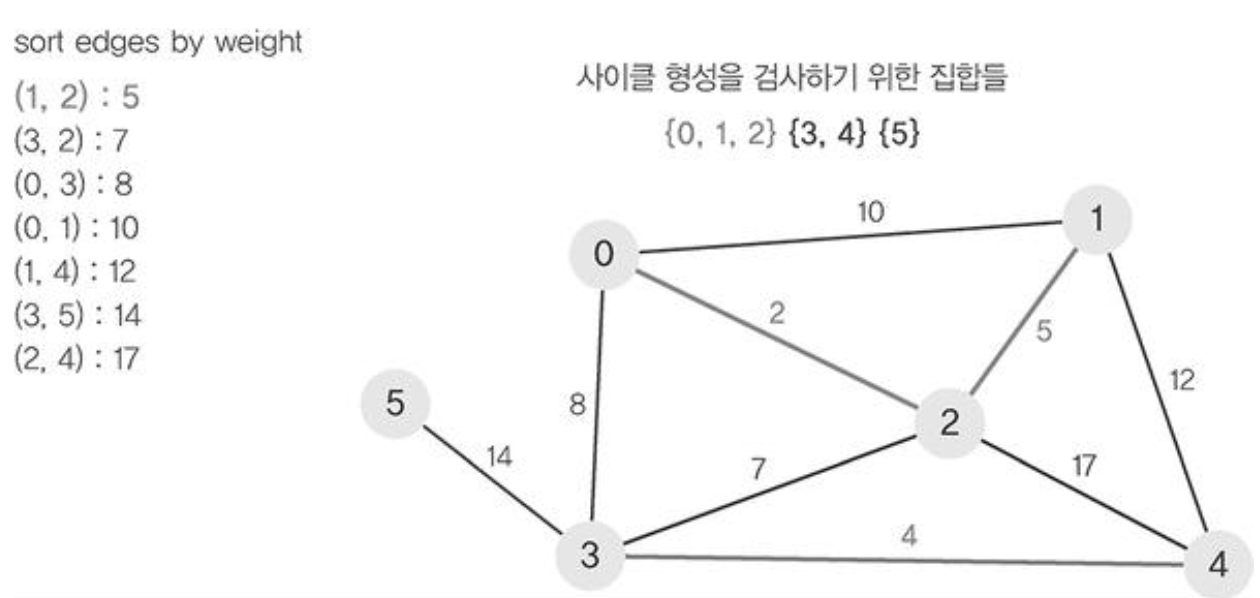
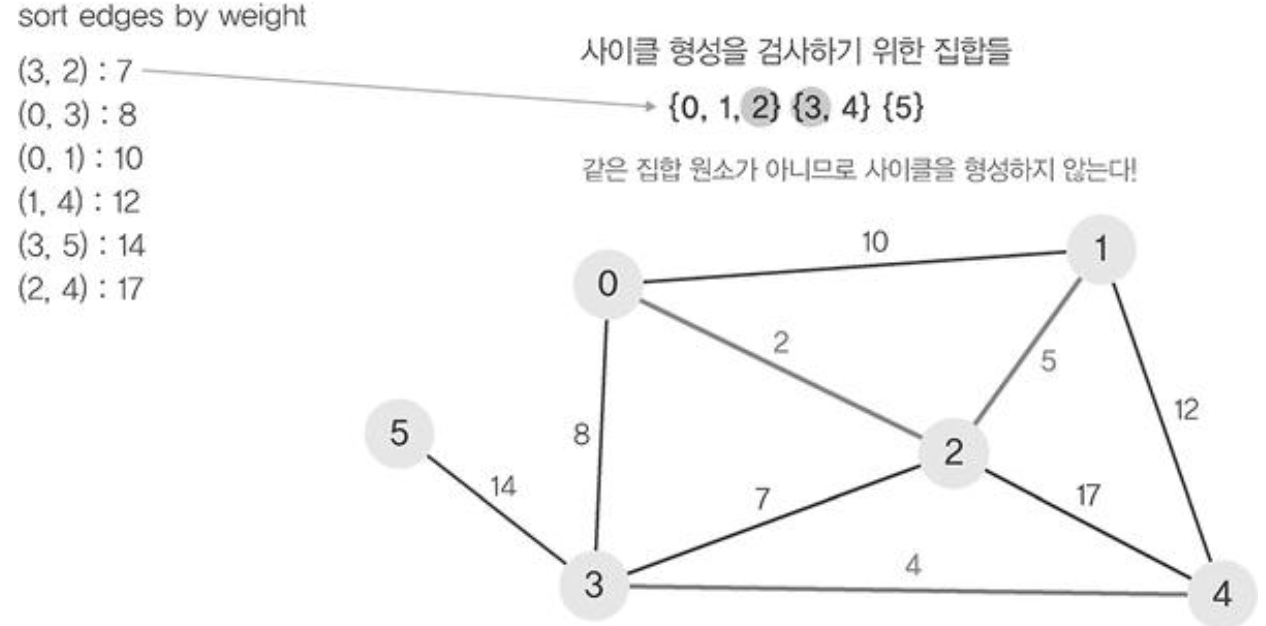
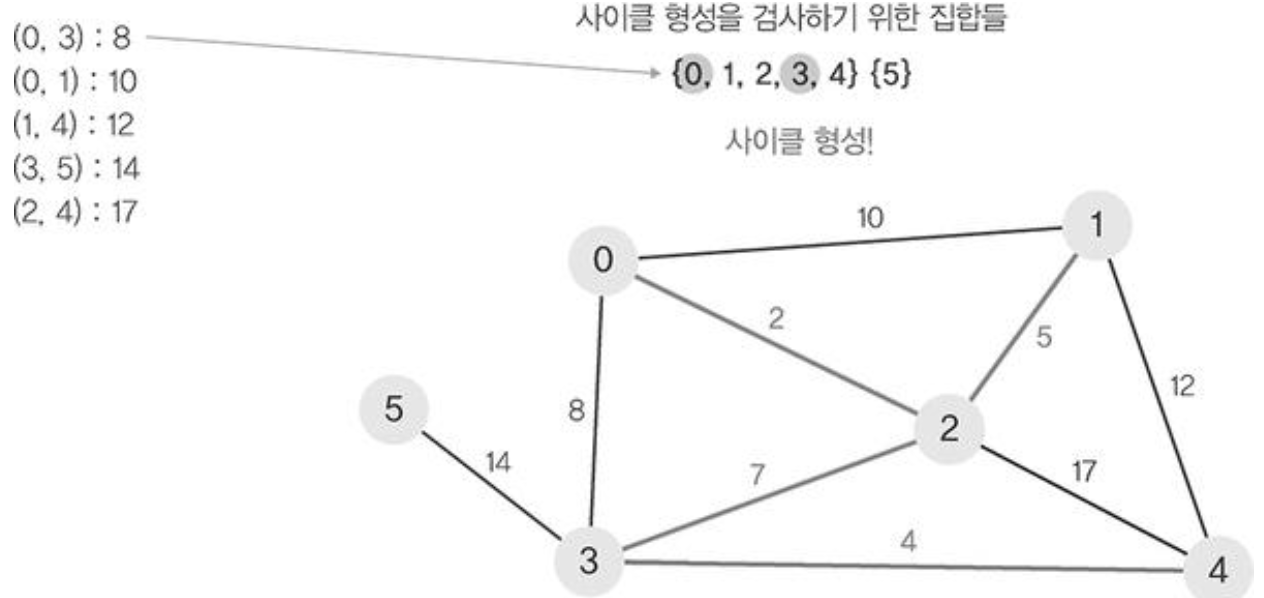
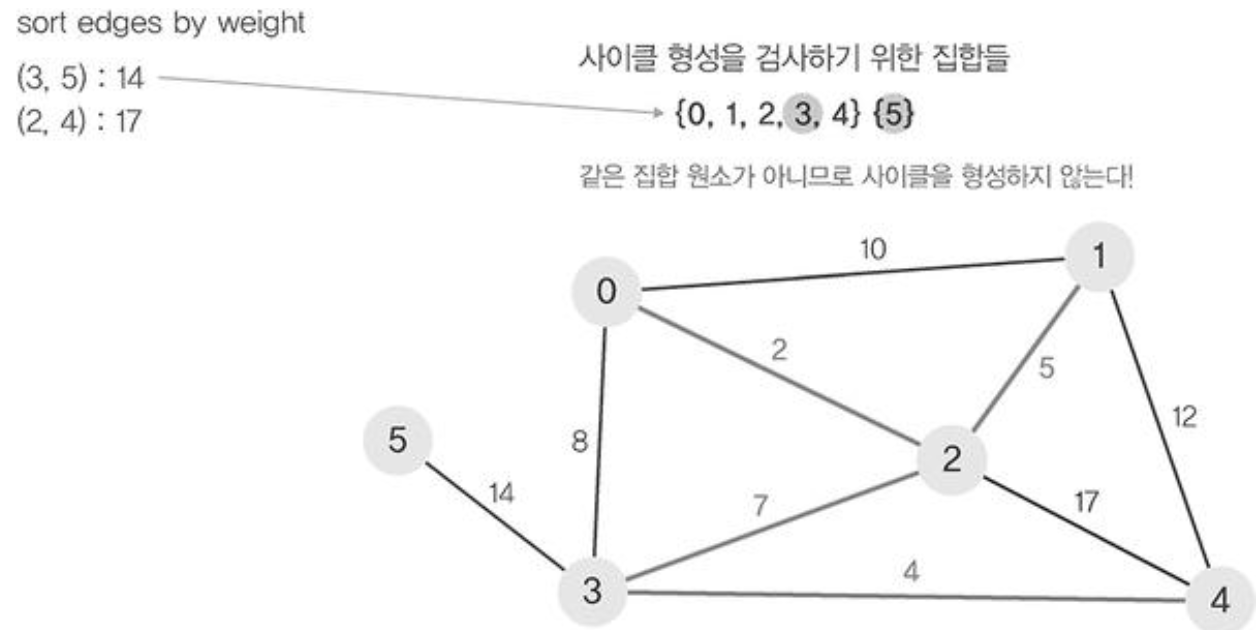
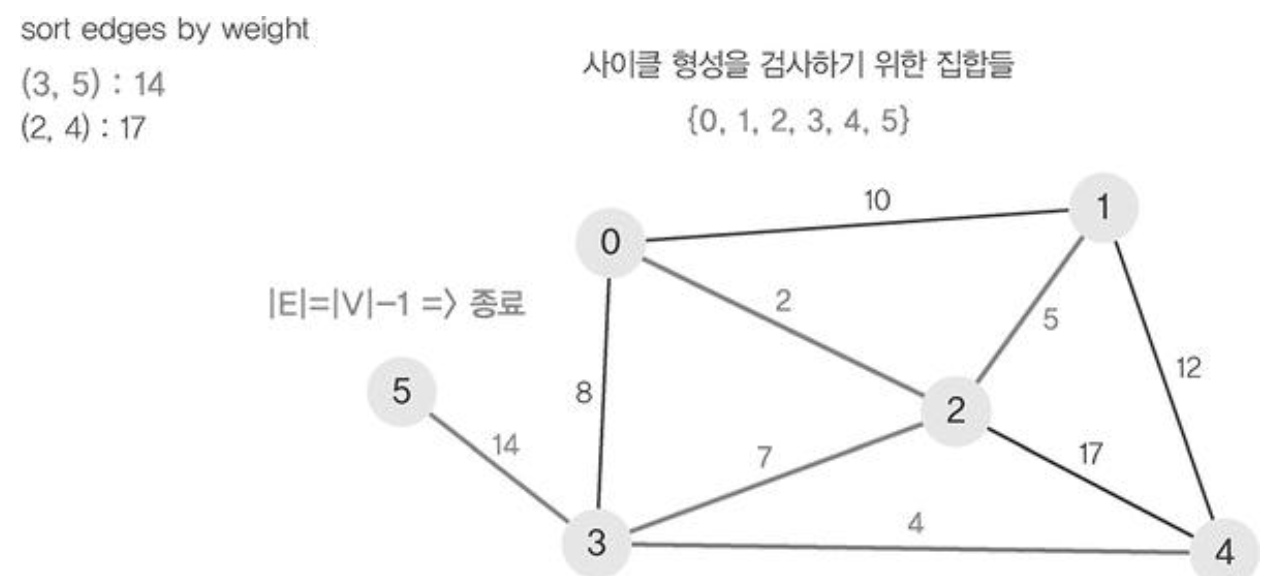
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다. 즉, 가장 낮은 가중치를 먼저 선택한다.
3. 사이클을 형성하는 간선을 제외한다.
4. 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.

사이클이 형성되는지 어떻게 확인하지?

• 서로 다른 두 집합을 병합하는 Union 연산, 집합 원소가 어떤 집합에 속해있는지 찾는 Find 연산을 활용한다.

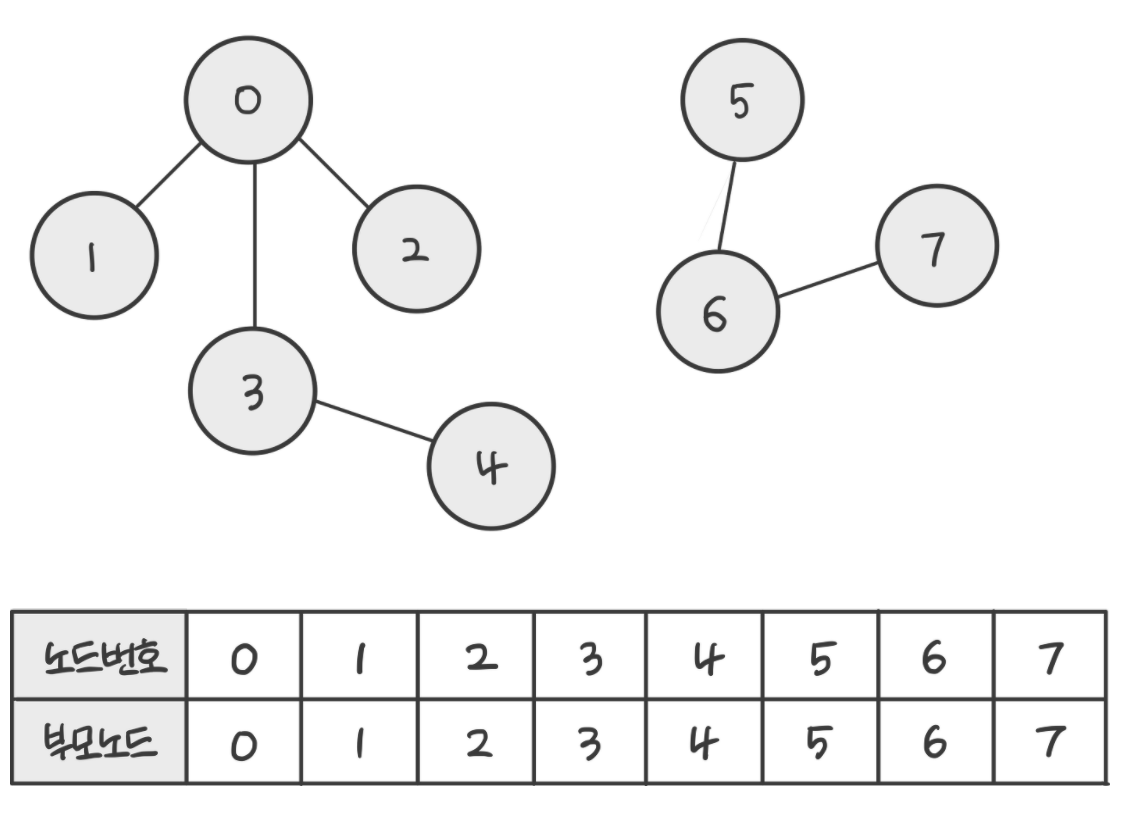
• parent 배열은 각 정점의 root node(부모)를 표현한 배열
• 간선 선택 전, 초기에는 자기 자신이 루트 노드가 되게 초기화 되어 있는 상태 (parent[i] = i)

• find 연산을 이용하여 에지(0,1)의 정점 0과 정점 1가 사이클이 형성하는지 확인한다.
• 사이클이 형성되지 않았다면 union연산을 이용하여 두집합을 하나로 합쳐준다.

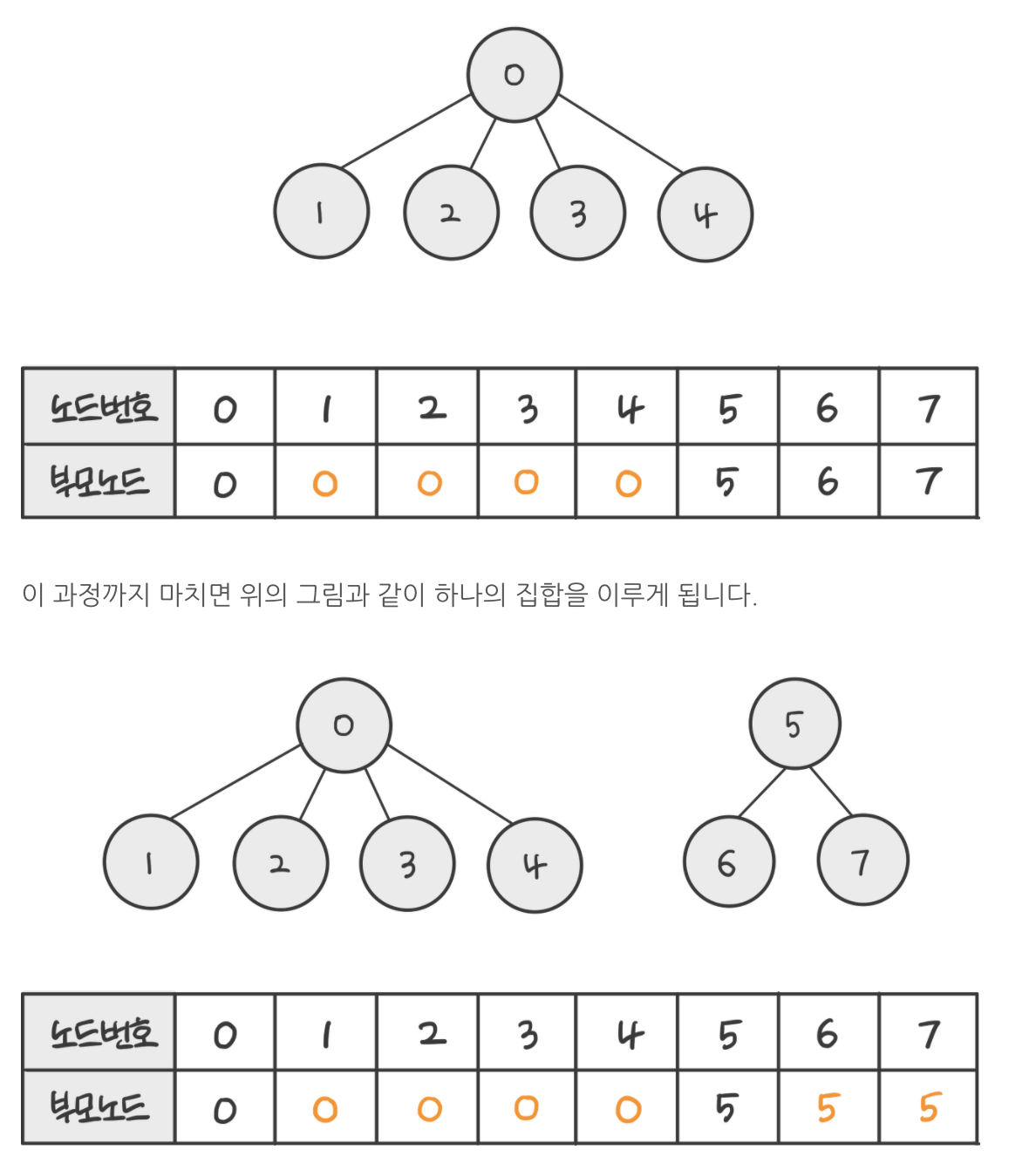
크루스칼 알고리즘 동작과정

from disjoint_set import DisjointSet

class Edge:
    # 시작정점, 끝정점, 가중치 초기화
    def __init__(self, u, v, w):
        self.u=u
        self.v=v
        self.w=w

class Graph:
    def __init__(self, vertex_num):
        self.adj_list=[[] for _ in range(vertex_num)]
        self.edge_list=[]

        self.vertex_num=vertex_num

    def add_edge(self, u, v, weight):
        self.adj_list[u].append(v)
        self.adj_list[v].append(u)

        self.edge_list.append(Edge(u, v, weight))

    def MST_kruskal(self):
        mst=Graph(self.vertex_num)     ## 최종적으로 만들 최소비용 신장 트리    
        ds=DisjointSet(self.vertex_num)  ## 사이클 형성 검사를 할 정접 집합
        self.edge_list.sort(key=lambda e: e.w)  ## 가중치에 따라 에지 정렬
        mst_edge_num=0
        edge_idx=0  ## 정렬된 에지 리스트에서 인덱스

        while mst_edge_num < self.vertex_num-1:
            edge=self.edge_list[edge_idx]
            if ds.collapsing_find(edge.u) != ds.collapsing_find(edge.v):
                ## find 연산을 활용하여 집합 원소가 어떤 집합에 속해있는지 확인
                mst.add_edge(edge.u, edge.v, edge.w)
                ds.weighted_union(ds.collapsing_find(edge.u), ds.collapsing_find(edge.v))
                # union 연산을 활용하여 두집합 병합
                mst_edge_num+=1
            edge_idx+=1

        return mst

    def print_edges(self):
        for edge in self.edge_list:
            print("({}, {}) : {}".format(edge.u, edge.v, edge.w))

if __name__=="__main__":
    g=Graph(6)

    g.add_edge(0, 1, 10)
    g.add_edge(0, 2, 2)
    g.add_edge(0, 3, 8)
    g.add_edge(1, 2, 5)
    g.add_edge(1, 4, 12)
    g.add_edge(2, 3, 7)
    g.add_edge(2, 4, 17)
    g.add_edge(3, 4, 4)
    g.add_edge(3, 5, 14)

    mst=g.MST_kruskal()

    mst.print_edges()

class DisjointSet:
    def __init__(self, vnum):
        self.parent=[-1 for _ in range(vnum)]

    def simple_find(self, i):
        while self.parent[i] >= 0:
            i=self.parent[i]
        return i

    def simple_union(self, i, j):
        self.parent[i]=j

    def collapsing_find(self, i):
        root=trail=lead=None
        # 루트를 찾는다.
        root=i
        while self.parent[root] >= 0:
            root=self.parent[root]

        # 모든 노드를 루트의 자식으로 만든다
        trail=i
        while trail != root:
            lead=self.parent[trail]
            self.parent[trail]=root
            trail=lead

        return root

    def weighted_union(self, i, j):
        """
        paremeters i, j must be roots!
        if size[i] < size[j] then parent[i]=j
        """
        #abs(parent[i])=size[i]
        #temp_cnt는 음수이고 size[i] + size[j]
        temp_cnt=self.parent[i]+self.parent[j]

        # 각 집합이 가진 노드 개수를 비교하여 노드개수가 많은 집합에 노드 개수가 적은 집합을 자식으로 병합
        #size[i] < size[j]
        if self.parent[i] > self.parent[j]:
            self.parent[i]=j
            self.parent[j]=temp_cnt
        #size[i] > size[j]
        else:
            self.parent[j]=i
            self.parent[i]=temp_cnt

if __name__=="__main__":
    ds=DisjointSet(5)

    # ds.simple_union(1, 2)
    # ds.simple_union(4, 2)
    # ds.simple_union(3, 0)
    # print(ds.parent)
    
    # for i in range(5):
    #     print("parent[{}] : {}".format(i, ds.simple_find(i)))

    ds=DisjointSet(5)
    ds.parent[2]=-5
    ds.parent[4]=2
    ds.parent[0]=4
    ds.parent[1]=0
    ds.parent[3]=1
    print(ds.parent)
    print("the root is {}".format(ds.collapsing_find(3)))
    print(ds.parent)
    

프림 알고리즘

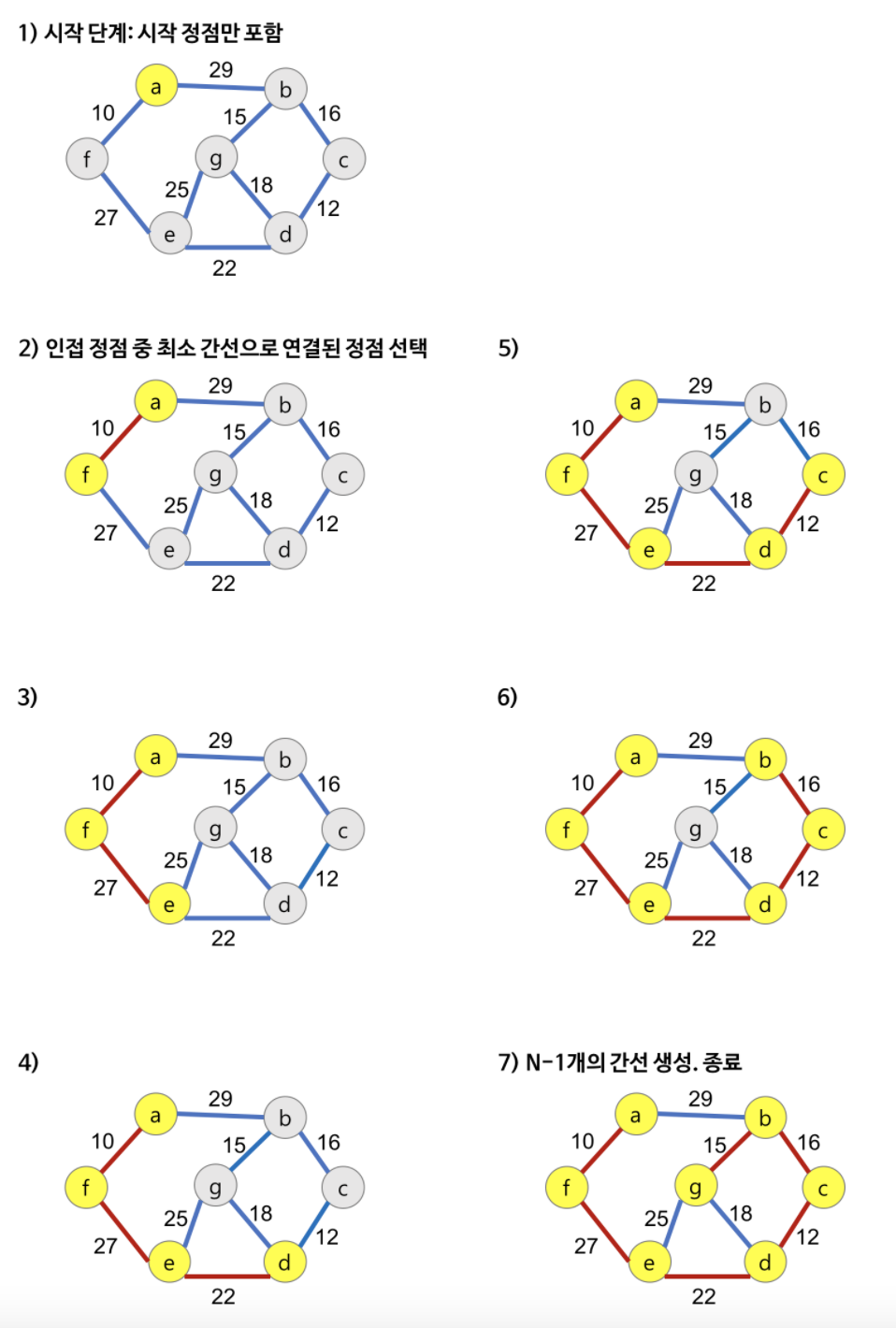
• 시작 정점을 선택한 후, 정점에 인접한 간선 중 최소 간선으로 연결된 정점을 선택하고, 해당 정점에서 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식

• Kruskal’s algorithm 과 Prim’s algorithm 비교

• 둘다, 탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)

• Kruskal’s algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구함

• Prim’s algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함

프림 알고리즘 동작과정

import math
from min_heap import Element, MinHeap

class Edge:
    def __init__(self, u, v, w):
        self.u=u
        self.v=v
        self.w=w

class Graph:
    def __init__(self, vertex_num):
        self.adj_list=[[] for _ in range(vertex_num)]
        self.edge_list=[]

        self.vertex_num=vertex_num

    def add_edge(self, u, v, w):
        # (정점, 에지의 가중치)를 인접 리스트에 추가
        self.adj_list[u].append((v, w))
        self.adj_list[v].append((u, w))

        self.edge_list.append(Edge(u, v, w))

    def MST_prim(self):
        mst=Graph(self.vertex_num)

        w_list=[math.inf for _ in range(self.vertex_num)]
        # w_list = [inf,inf,inf,inf,inf,inf]
        TV=set()
        h=MinHeap()

        # Element 객체: 가중치를 키로 사용한다.
        for i in range(1, self.vertex_num):
            h.push(Element(i, math.inf, None))

        w_list[0]=0
        h.push(Element(0, 0, None))
        
        while not h.is_empty():
            elem_v=h.pop()
            v=elem_v.v 
            w=elem_v.w 
            _from=elem_v._from
            
            TV.add(v)
            if _from != None:
                mst.add_edge(v, _from, w)
            
            adj_v=self.adj_list[v]
            # 노드 0일 경우 
            # adj_v = [(1,10),(2,2),(3,8)]
            for u, w_u_v in adj_v:
                if u not in TV and w_u_v < w_list[u]:
                    # TV 이전에 노드를 방문했는지 체크 하기 위한 용도
                    w_list[u]=w_u_v
                    h.decrease_weight(Element(u, w_u_v, v))
                    # u : 끝정점, w_u_v : 가중치, v : 시작정점

        '''
        # 새로운 가중치가 기존 가중치보다 작다면 decrease_weight 연산
        def decrease_weight(self, new_elem):
            cur=self.pos[new_elem.v]

            while cur!= 1 and new_elem.w < self.arr[self.parent(cur)].w:
                self.arr[cur]=self.arr[self.parent(cur)]
                self.pos[self.arr[cur].v]=cur    

                cur=self.parent(cur)

            self.arr[cur]=new_elem
            self.pos[new_elem.v]=cur
        '''
        
        '''
        결과값
        (2, 0) : 2
        (1, 2) : 5
        (3, 2) : 7
        (4, 3) : 4
        (5, 3) : 14
        '''
        return mst

    def print_edges(self):
        for edge in self.edge_list:
            print("({}, {}) : {}".format(edge.u, edge.v, edge.w))

if __name__=="__main__":
    g=Graph(6)

    g.add_edge(0, 1, 10)
    g.add_edge(0, 2, 2)
    g.add_edge(0, 3, 8)
    g.add_edge(1, 2, 5)
    g.add_edge(1, 4, 12)
    g.add_edge(2, 3, 7)
    g.add_edge(2, 4, 17)
    g.add_edge(3, 4, 4)
    g.add_edge(3, 5, 14)

    mst=g.MST_prim()

    mst.print_edges()