Topological Sort

• 위상 정렬이란 무엇인가?
• 위상 정렬 알고리즘 구현하기

---

1. Topology

• 지속적인 변형(늘어남, 비틀림, 구겨짐, 굽힘)하에 보존되는 기하학적 특성과 관련되는 수학의 한 분야
• 모든 종류의 연속성을 정의할 수 있는 구조

---

2. Topological Sort

• 따라서 위상 정렬^{Topological Sort}이란, 정렬 중에 연속성, 연결이라는 속성의 정렬
• EX)
  • 대학교 선수과목 (B과목은 그냥 수강 가능하지만, A과목은 B과목 수강 이후에만 수강 가능하다.)
    • 중급 회계는 회계원리를 수강한 학생만 수강 가능
    • 알고리즘은 C 언어를 수강한 학생만 수강 가능 (?)

---

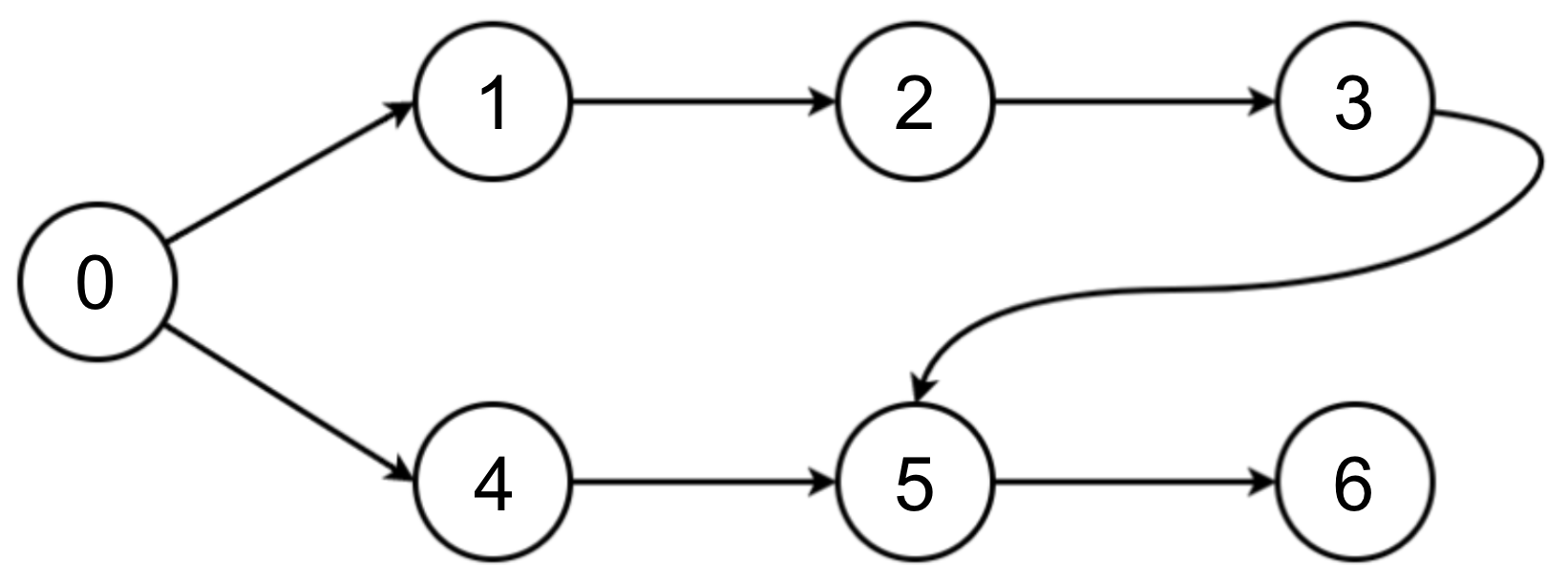
3. DAG

• 위상 정렬이 되기위한 조건
  • Direct Acycle Graph
  • 방향이 있다
  • 싸이클이 없다
  • 방향은 있으며, 싸이클이 없는 그래프

---

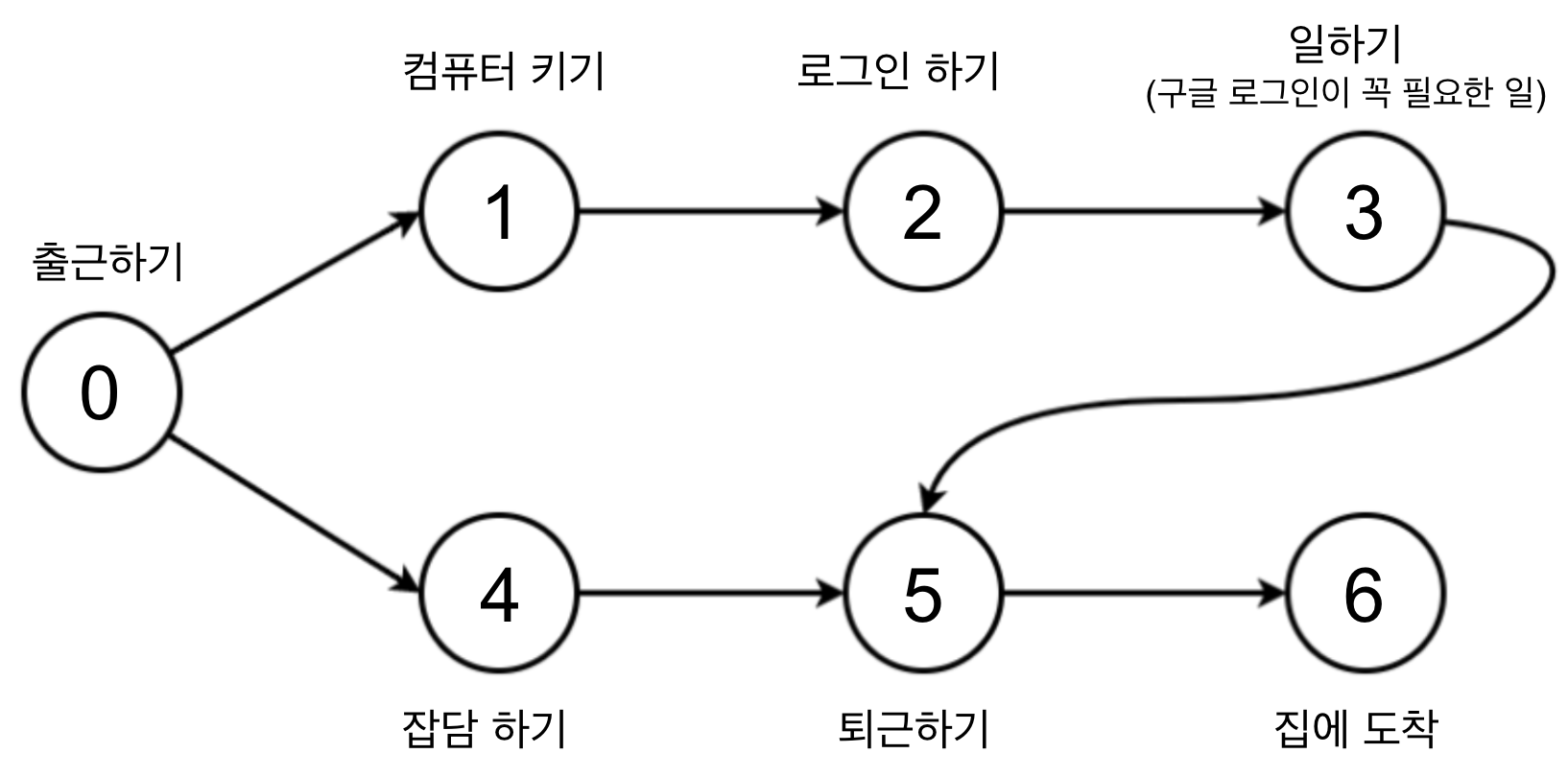
4. Kylie의 하루

• 가장 먼저 출근을 합니다.
• 마지막은 퇴근을 하고 집에 도착합니다.
• 퇴근을 하기 전에는 일을 합니다.
• 일을 하기 위해선 구글 로그인이 필요하고, 구글 로그인은 컴퓨터를 켜야 가능합니다.
• 퇴근 하기 전에 잡담도 합니다.
• 카일리의 하루를 위상 정렬으로 나타내기
  • 출근하기 → 컴퓨터 키기 → 로그인 하기 → 일하기 → 잡담하기 → 퇴근하기 → 집에 도착
  • 출근하기 → 컴퓨터 키기 → 로그인 하기 → 잡담하기 → 일하기 → 퇴근하기 → 집에 도착
  • 출근하기 → 잡담하기 → 컴퓨터 키기 → 로그인 하기 → 일하기 → 퇴근하기 → 집에 도착

---

5. 위상 정렬 알고리즘 구현하기

Stack

• LIFO(Last In First Out)
  1. 위상 정렬을 시작하기 전에 각 정점(vertex)와 진입 차수(in-degree) 정보를 저장한다.
  2. 진입 차수(in-dgree)가 0인 정점(vertex)을 스택에 삽입한다.
  3. 스택에 들어 있는 것을 pop으로 꺼내고, 해당 노드에서 갈 수 있는 노드의 진입차수를 1 감소 시키고, 진입 차수가 0이라면 해당 노드를 스택에 넣는다.
  4. 스택이 비어질때 까지 3번 과정을 반복한다.
     • 만약 모든 원소(정점, 노드)를 방문하기 전에 스택이 빈다면 사이클이 존재하는 것이고
     • 모든 원소를 반뭉했다면 스택에서 꺼낸 숫자가 위상 정렬의 결과가 된다.

Queue

• FIFO(First In Fist Out)

Operation (연산)

class DAG:
    def __init__(self, vertex_num):
        self.adj_list = [[] for _ in range(vertex_num)]
        self.visited = [False for _ in range(vertex_num)]

    def add_edge(self, u, v):
        # u : tail, v : head
        self.adj_list[u].append(v)

    def topological_sort(self):
        # 위상 정렬을 담당하는 메소드 
        self.init_visited()
        ts_list = []
        for i in range(len(self.visited)):
            if not self.visited[i]:
                self.dfs(i, ts_list)
        ts_list.reverse()
        return ts_list

    def init_visited(self):
        for i in range(len(self.visited)):
            self.visited[i] = False

    def dfs(self, v, ts_list):
        self.visited[v] = True
        adj_v = self.adj_list[v]
        for u in adj_v:
            if not self.visited[u]:
                self.dfs(u, ts_list)
        ts_list.append(v)

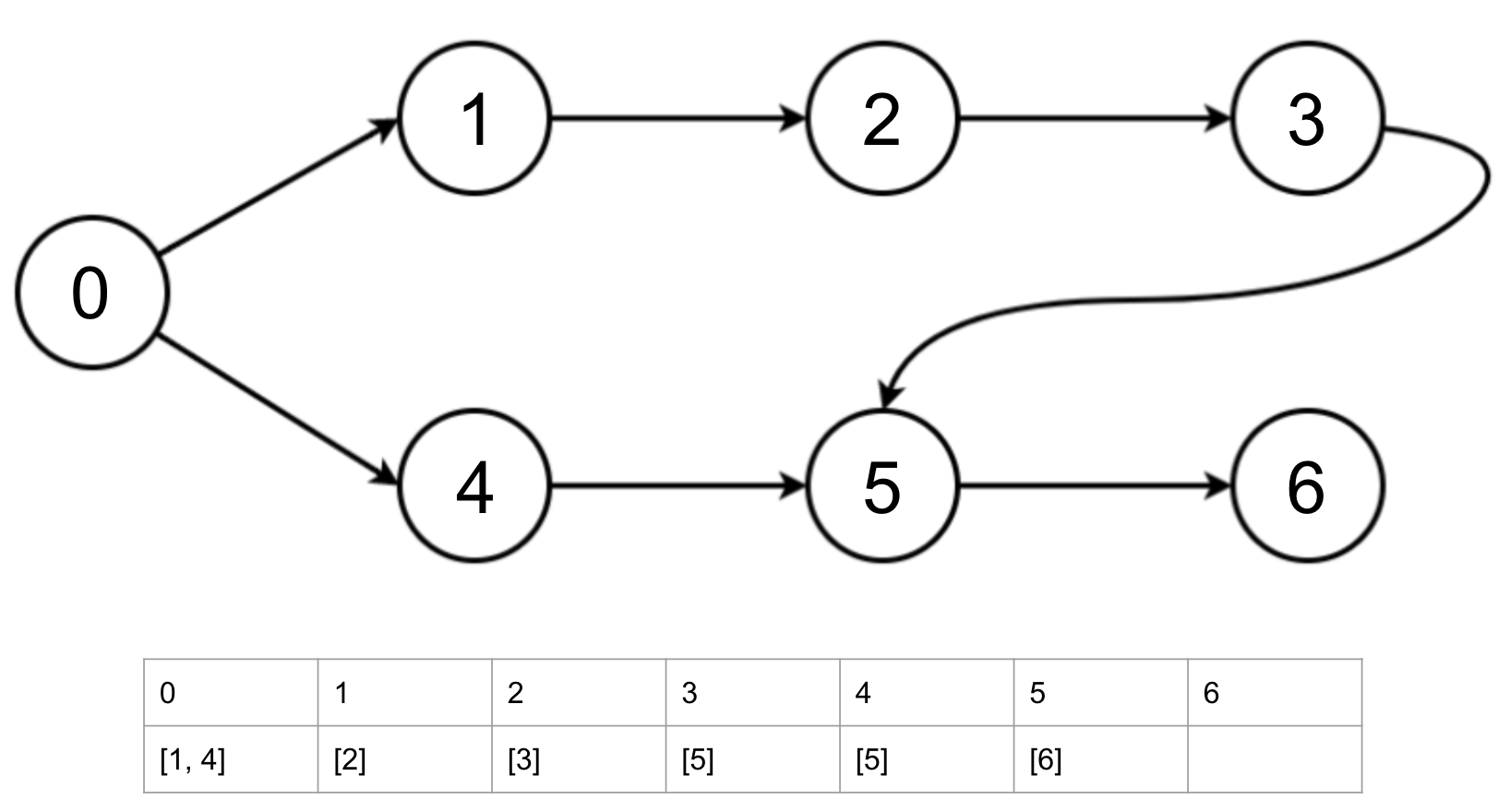
if __name__ == "__main__":
    d = DAG(7)
    d.add_edge(0, 1)
    d.add_edge(0, 4)
    d.add_edge(1, 2)
    d.add_edge(2, 3)
    d.add_edge(3, 5)
    d.add_edge(4, 5)
    d.add_edge(5, 6)

    ts_list = d.topological_sort()

    for i in ts_list:
        print(i, end=" ")  

0 4 1 2 3 5 6

위상 정렬은 어디에 쓰이나요?

• 스프레드 시트에서 어떤 셀 값이 변경 되었을 때, 이 값이 의존하는 모든 셀 값을 업데이트 할 때 쓰인다고 합니다.