💡 최단 경로 알고리즘

💭 하나의 출발점에서 나머지 모든 목적지에 대한 최단 경로를 구하는 알고리즘

• 다익스트라 알고리즘
• 벨만 포드 알고리즘

💭 모든(출발지, 목적지) 쌍에 대한 최단 경로를 구하는 알고리즘

• 플로이드 워셜 알고리즘
  • 다이나믹 프로그래밍의 대표적인 예

📌 다익스트라

• 다이나믹 프로그램을 활용한 대표적인 최단 경로 탐색 알고리즘
• 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줌
• 인공위성 gps 소프트웨어 등에서 가장 많이 사용
• 프림 알고리즘과 매우 유사
  • 탐욕 알고리즘에 기반
• 음수 가중치를 인정하지 않음
  • 음수 간선이 있으면 데이크스트라 대신에 벨만-포드 알고리즘이나 SPFA를 사용
  • 자세한 설명은 뒷부분에서 설명할 예정
• 현실 세계에서는 음의 간선이 존재하지 않기 때문에 다익스트라는 현실 세계에 사용하기 매우 적합한 알고리즘 중 하나

🔎 다이나믹 프그래밍으로 말하는 이유 🔍
- 최단거리는 여러 개의 최단 거리로 이루어져 있음
- a 에서 b 로 가고 b 에서 c 로 가고 c 에서 d 로 가는 경로가 a 에서 d 로 가는 최단 경로라면
그 과정 속에 있던 a 에서 b 로 가는 각 경로들도 최소가 되어야 함
- 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용하는 특징이 있음

> 위와 같은 특징 때문에 작은 문제가 큰 문제 속에 비슷한 형태로 포함되어 있는 다이나믹 프로그래밍
형태로 볼 수 있습니다.

🔎 그리디 알고리즘으로 말하는 이유 🔍
> 정렬을 사용하기 때문에 정렬 이후에 가장 적은 것을 선택하는 것이 알고리즘에 포함되기에 그리디 알고리즘
으로도 분류될 수 있습니다.

📌 다익스트라 - Relax 연산

본격적인 다익스트라 알고리즘 설명에 앞서 가장 핵심적인 Relax 연산에 대해 먼저 설명하겠습니다.

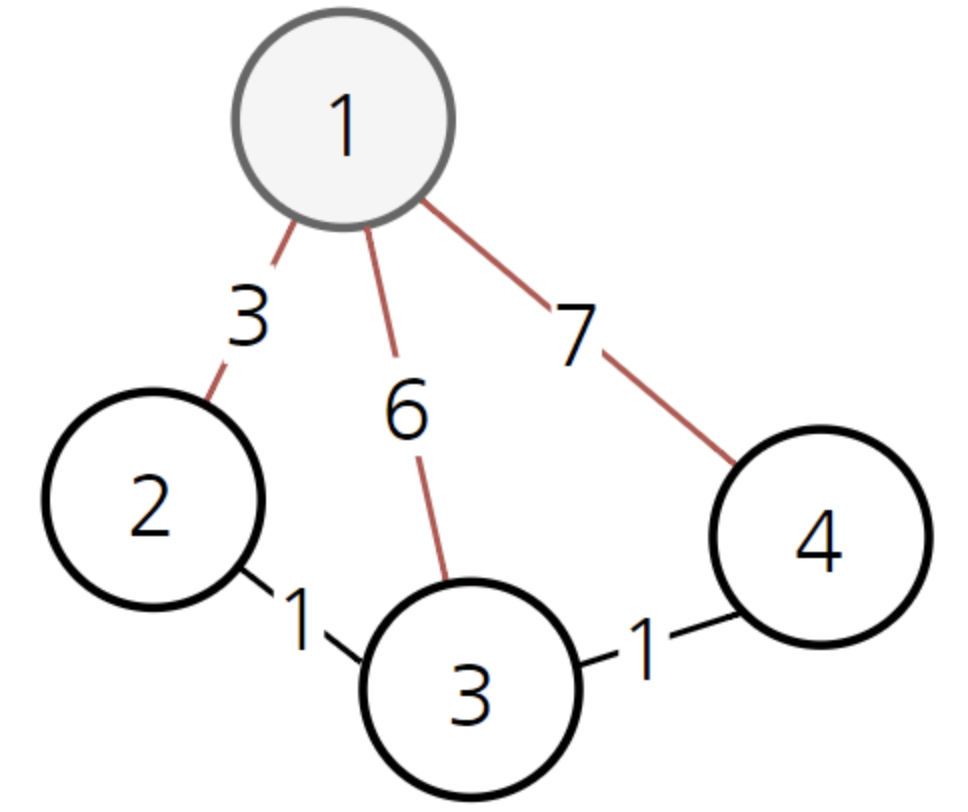
1부터 다른 모든 노드로 가는 최단 경로를 구한다고 가정해봅시다.

현재 접근할 수 있는 노드는 1 밖에 없다고 가정한다면, 1 에 인접노드인 2, 3, 4 까지의 최단 거리는
각각 3, 6, 7 로 볼 수 있습니다.

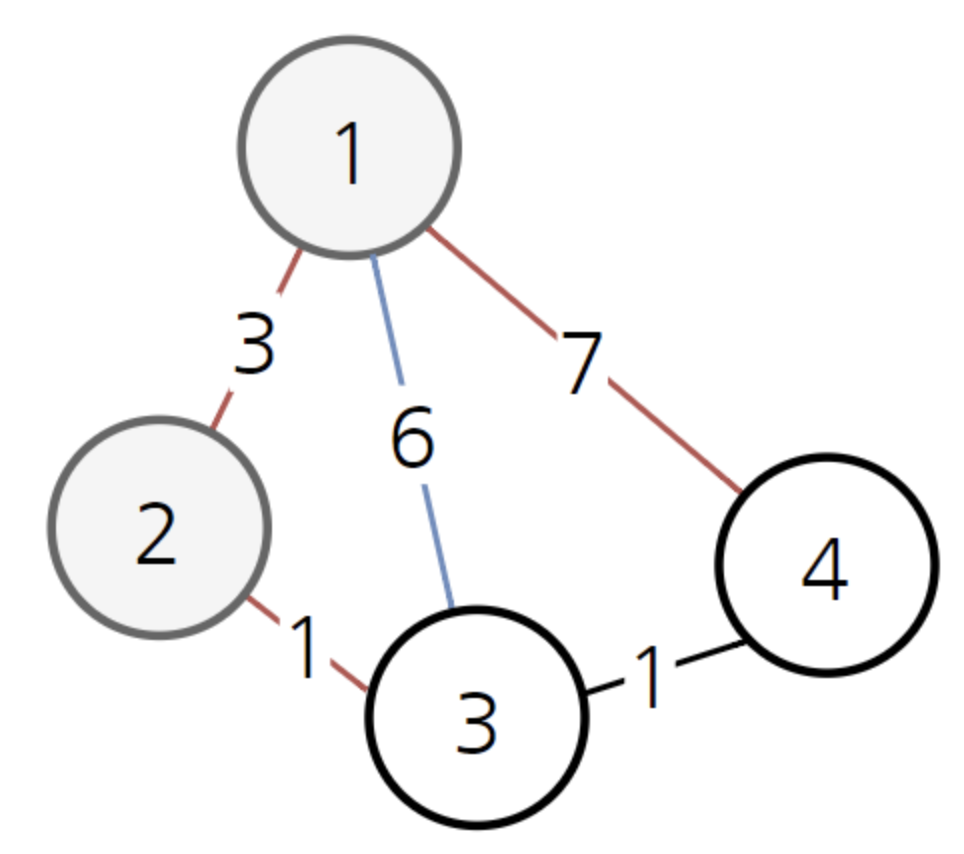
다음으로 노드 2 를 처리할 수 있게 되었다면,

1 - 3 (6) 의 비용보다 1 - 2 - 3 (3 + 1) 을 통한 경로가 비용이 더 저렴한 것을 알 수 있습니다.

이 때, 알고리즘에서는 기존에 알고 있던 3 으로 가는 최소 비용을 6에서 4 로 새로 갱신하게 됩니다.

이렇게 다익스트라 알고리즘은 현재까지 알고 있던 최단 경로를 갱신하며 노드 별 최단 경로를 찾게 되는데
이러한 연산을 relax 라 하며, 이런 연산을 하는 것을 relaxation 이라 합니다.

📌 다익스트라 알고리즘 동작 과정

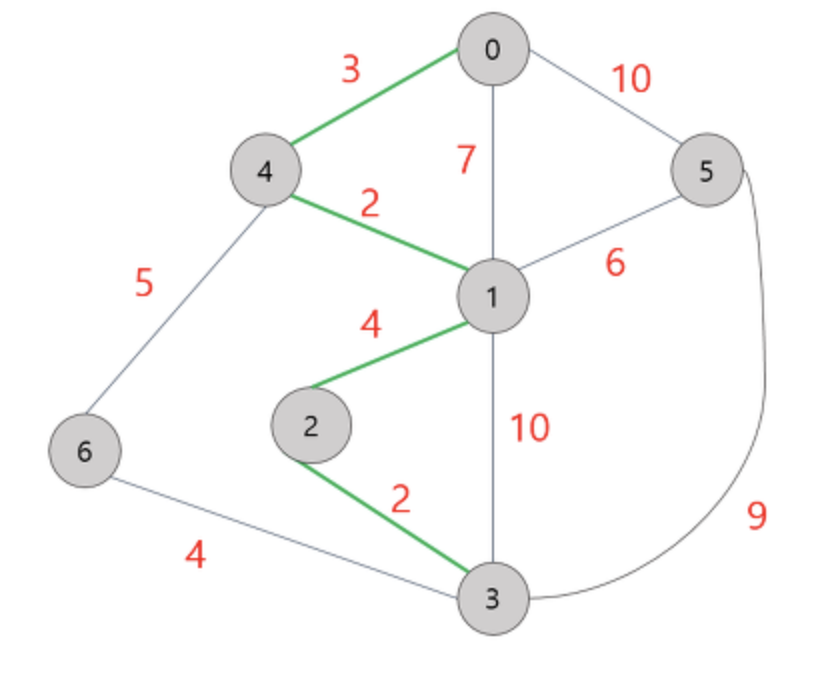
위의 그래프를 통해 다익스트라 알고리즘의 동작 과정에 대해 자세히 살펴보겠습니다.

가중치는 가중치 인접 행렬 이라 불리는 2차원 배열에 저장합니다. 이때 자기 자신의 대한 가중치는 0으로 표시합니다. 자기 자신에 대한 가중치 값이 0 으로 나타내기 때문에 노드간 간선이 없음을 나타낼 때 는 0 이라는 값 대신 무한대 의 값을 사용합니다.

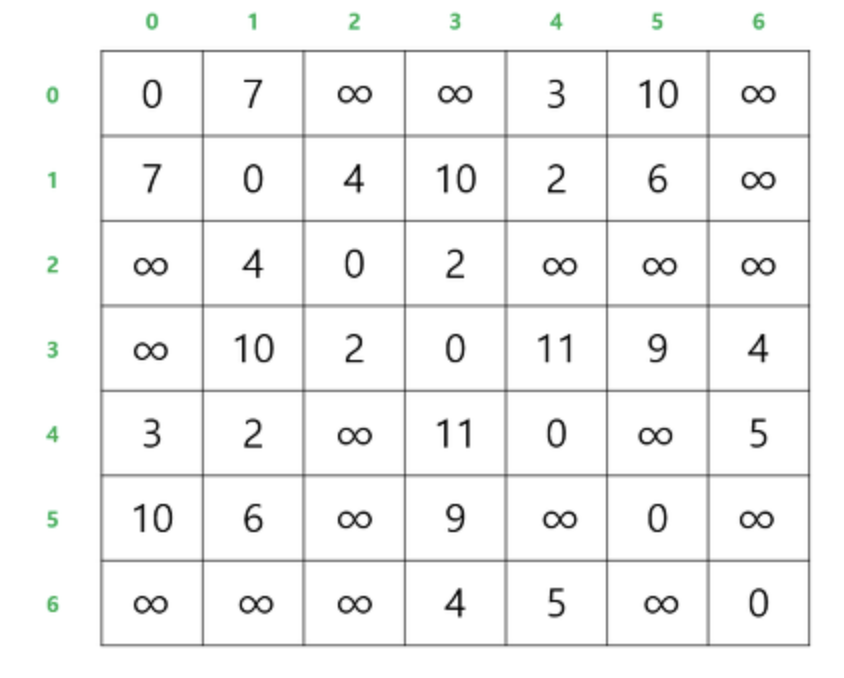
다익스트라 알고리즘에서는 시작 정점에서 집합 S 에 있는 정점만을 거쳐서 다른 정점으로 가는
최단 거리를 기록하는 배열이 반드시 있어야 합니다.

• 집합 S 는 최단 거리에 해당하는 정점이 하나씩 추가됩니다.
• 집합 S 에 속한 정점들은 relax 연산으로 인해 최단 거리가 구해진 정점들이기에 추가된 이후부턴
  새로 갱신되지 않습니다.
• 처음 시작 시 S = {v} 이며
  • v는 시작 정점을 의미합니다.
  • 최단 거리가 발견되는 정점들이 이후에 집합 S에 하나씩 추가됩니다.
  • 집합 S 에 모든 정점이 속하게 될 경우 알고리즘은 종료됩니다.
    
    

최단 거리를 기록하는 1차원 배열의 이름을 distance 라 하겠습니다.
이 때 시작 정점을 v 라고 한다면, distance[v]=0 이며 다른 정점에 대한 distance 값은 시작 정점과 해당 정점 간의 가중치가 됩니다. 위에 보여드렸던 가중치 인접 행렬을 weight 라 했을 때 $distance[w] = weight[v][w]$ 로 말할 수 있습니다.

알고리즘의 매 단계에서 집합 S 안에 있지 않은 정점 중에서 가장 distance 값이 작은 정점을 S에 추가하게 됩니다.
새로운 정점 u가 S에 추가되면, S에 있지 않은 다른 정점들의 distance 값을 수정합니다.

distance값은 relax 연산을 통해 그 최소값을 찾게 되는데 이는 다음과 같은 식으로 표현될 수 있습니다.

\[distance[w] = min(distance[w], distance[u] + weight[u][w])\]

이제 실제 다익스트라 알고리즘의 동작 과정에 대해 따라가보겠습니다.

시작정점을 0으로 잡았다고 가정해봅시다.

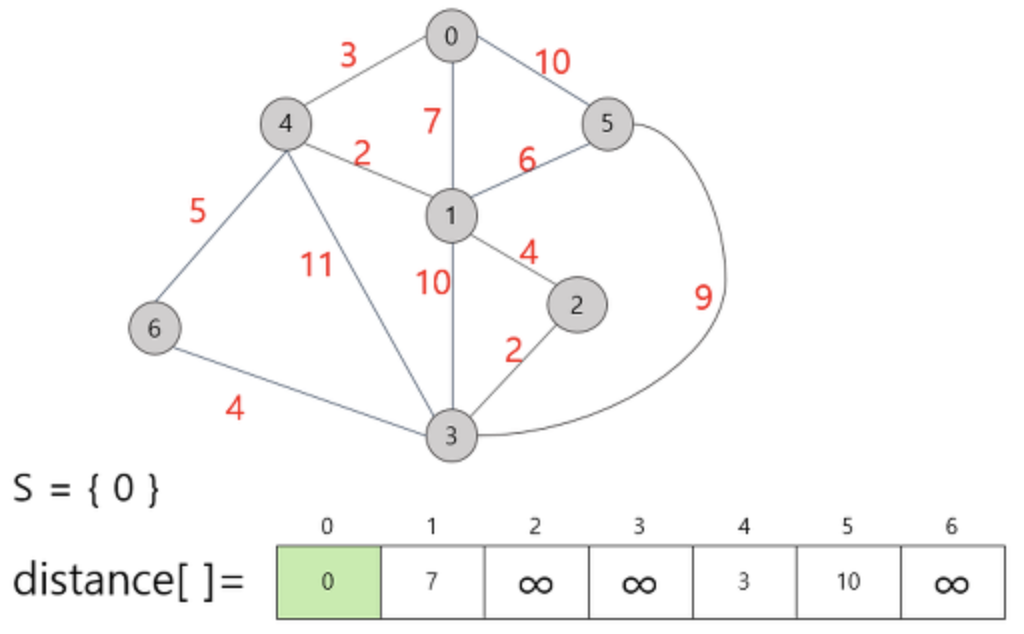
집합 S 에는 시작정점인 0 이 들어가 있습니다. 또한 distance 배열에는 자기자신의 비용은 0 이며
연결되어 있지 않는 정점들은 무한대로 표시되어 있습니다.

이제 정점 0 의 입장에서 가장 짧은 거리의 정점을 찾아보겠습니다.

우선 간선이 직접적으로 연결되어있지 않아서 비용이 무한대로 표시되어 있는 2, 3, 6이 제일 먼저 제외됩니다.

이 후, 인접정점인 4, 1, 5 정점 중 3으로 가장 적은 비용을 가지고 있는 정점 4가 집합 S에 추가됩니다.

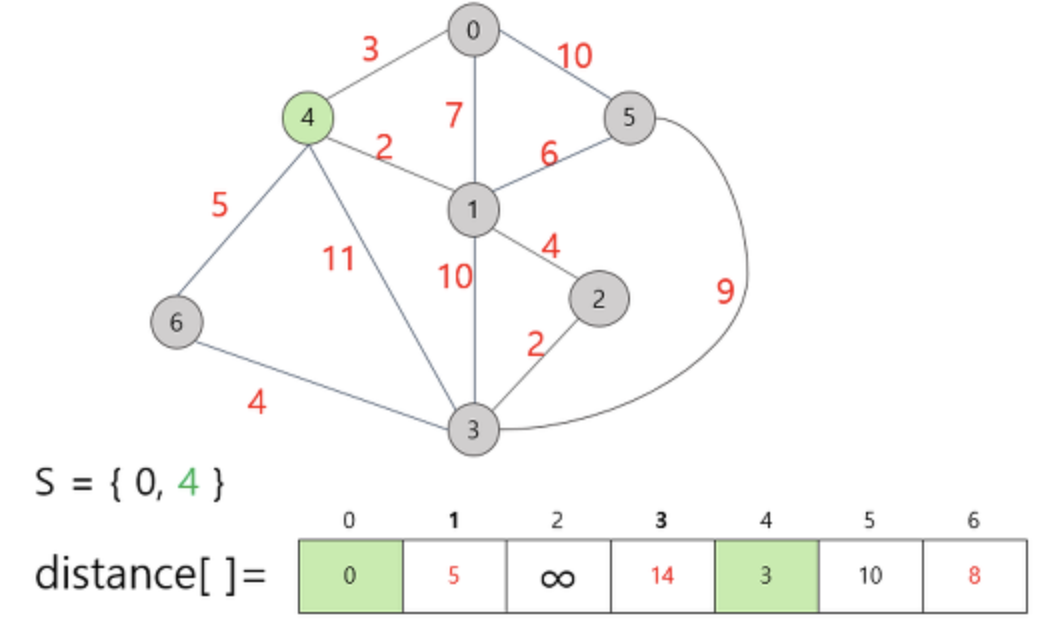
새로운 정점이 집합 S에 추가 되었으므로 다른 정점들의 distance 값이 변경됩니다.

정점 0 에서 간선이 이어져있지 않아 무한대로 표시되어있던 정점 3과 6이 정점 4를 통해서 접근이 가능해졌으므로
값이 새로 변경 됩니다.

또한 relax 연산을 통해 정점 1의 distance 값이 최소값으로 값이 변경 되었습니다.

다음으로 집합 S에 속하지 않은 정점 중 가장 적은 비용을 가지고 있는 정점 1 을 선택합니다.

정점 1을 집합 S에 새로 추가하고 마찬가지로 다른 정점들의 distance 값을 새로 변경합니다.

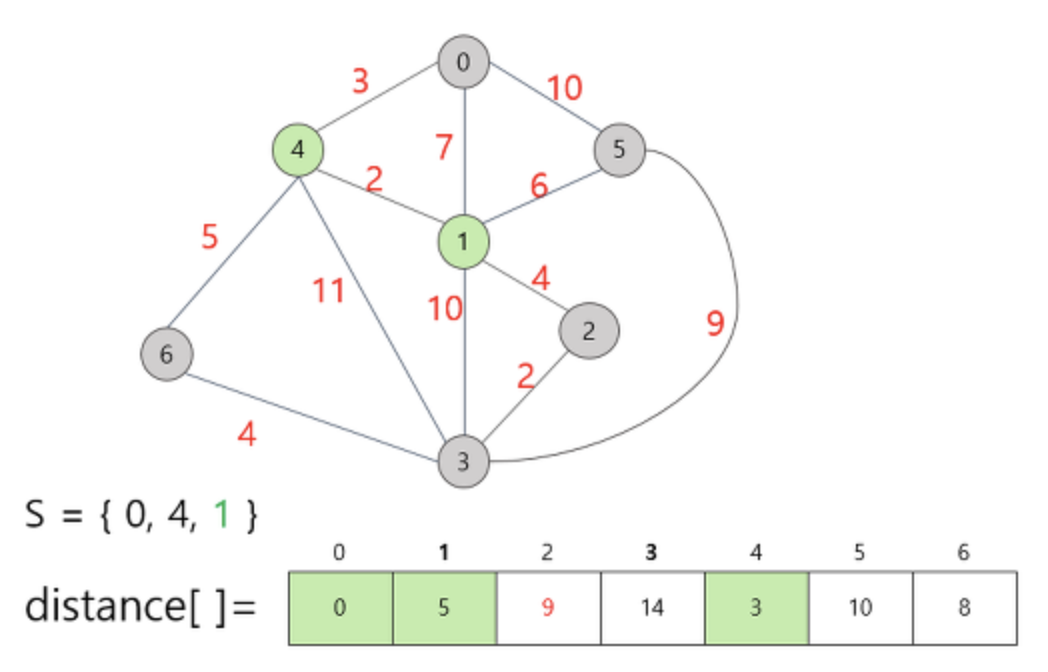
정점 2 에 대해 정점 1을 통해 접근이 가능하게 되었으므로 relax 연산을 통해 기존 무한대의 값에서 9라는 최소값을 새로 변경되었습니다.

다음으로 집합 S에 속하지 않은 정점 중 가장 적은 비용을 가지고 있는 정점 6을 선택하여 새로 S에 추가합니다.

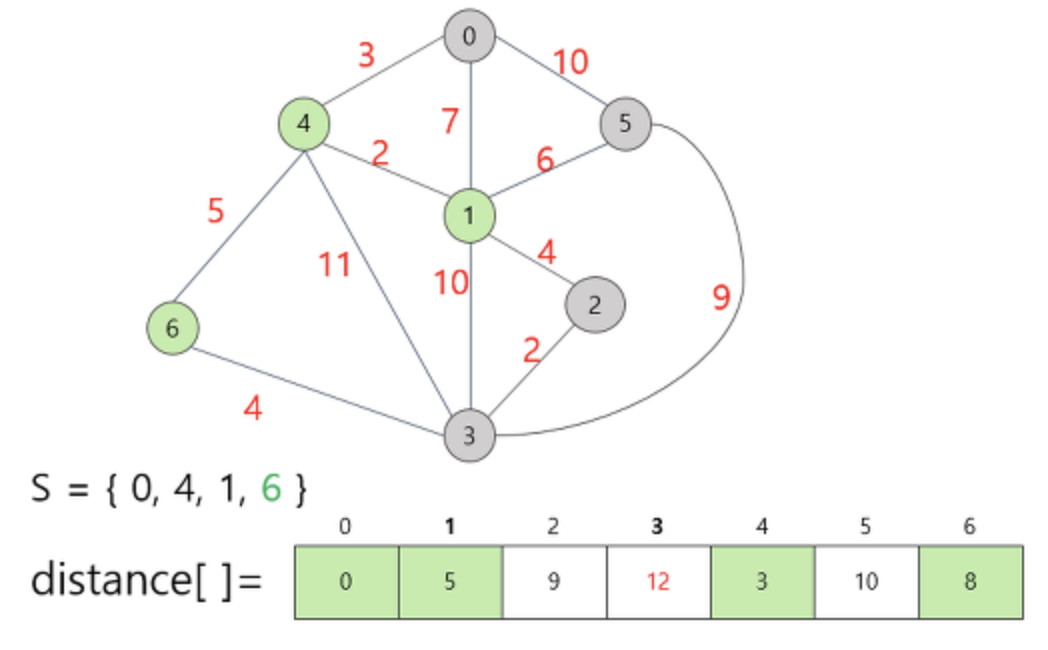
집합 S에 정점 6이 추가됨으로써 정점 3 에 대한 정보가 14 → 12 로 새로 변경되었습니다.

(distance[3] = min(distance[3], distance[6] + weight(6, 3) = min(14, 8 + 4) = 12 )

다음으로 집합 S에 속하지 않은 정점 중 가작 적은 비용을 가지고 있는 정점 2 를 선택하여 집합 S에 추가해줍니다.

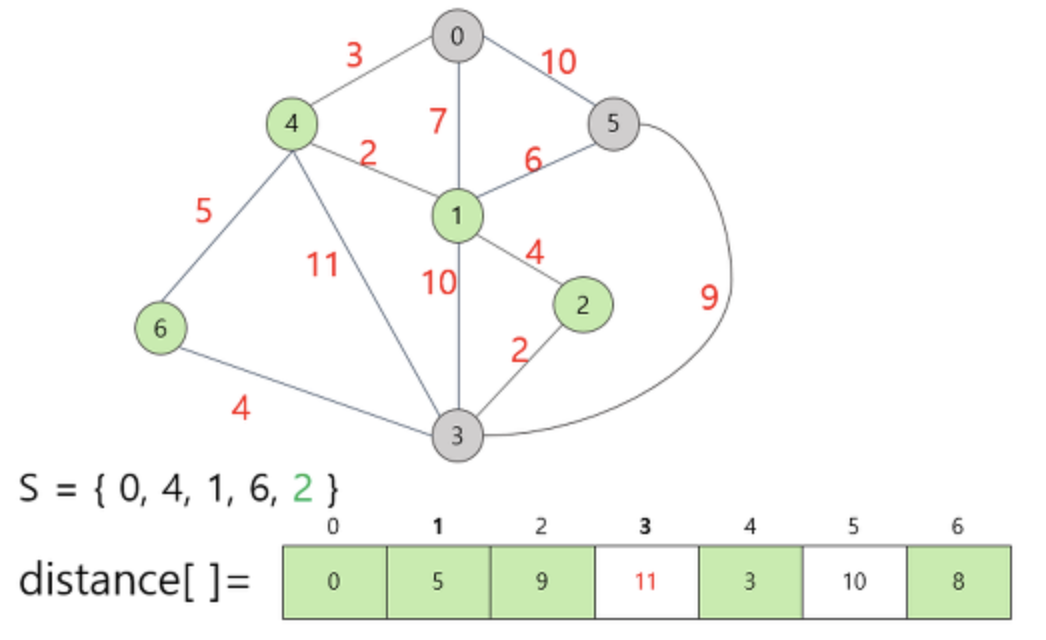
집합 S에 정점 2를 추가함으로써 정점 3에 대한 정보가 relax 연산을 통해 새로 변경되었습니다.

(distance[3] = min(distance[3], distance[2] + weight(2,3) = min(12, 9 + 2) = 11)

다음으로 가장 적은 비용을 가지고 있는 정점 5를 집합 S에 추가하고 위와 같은 과정을 거치며
정점 3까지 집합 S에 추가하면 다익스트라 알고리즘은 종료됩니다.

Code

위 예시는 이해를 돕기 위해 가장 간단한 표현 방식으로 설명한 예시입니다. 위의 방식대로 코드를 구현할 경우 시간복잡도가 $O(n^2)$ 을 가지기 때문에 효율적이지 않습니다. 이를 최소우선순위큐를 사용하면 최소우선순위큐에서 pop시 거리가 가장 적은 값이 나오기 때문에 시간복잡도를 $O(nlogn)$ 으로 만들 수 있습니다. 아래의 구현 코드는 이를 반영한 코드입니다.

from heapq import heappush, heappop

class MinPriorityQueue:
    def __init__(self):
        self.heap = []
    def push(self, item):
        heappush(self.heap, item)
    
    def pop(self):
        return heappop(self.heap)

class ShortestPath:
    def __init__(self, s, distance, p):
        self.source = s
        self.distance = distance
        self.p = p
    def print_shortest_path(self, dest):
        if self.source == dest:
            print(dest, end= " ")
            return
        if self.p[dest] != None:
            self.print_shortest_path(self.p[dest])
        else:
            print("There is no path")
            return
        print(dest, end=" ")

class Graph:
    BIG_NUMBER = 2000
    def __init__(self, vertex_num):
        self.adj_matrix = [[None for _ in range(vertex_num)] for _ in range(vertex_num)]
        self.vertex_num = vertex_num
    def add_edge(self, u, v, w):
        self.adj_matrix[u][v] = w


    def dijkstra(self, s):
        distance = [self.BIG_NUMBER for _ in range(self.vertex_num)]
        p = [None for _ in range(self.vertex_num)]

        S = set()
        pq = MinPriorityQueue()
        for i in range(self.vertex_num):
            pq.push((self.BIG_NUMBER, i))
        distance[s] = 0
        pq.push((0, s))

        while len(S) < self.vertex_num:
            d, v = pq.pop()
            print(d,v)
            
            if distance[v] != d:
                continue
        
            S.add(v)
            print(f'S: {S}')
            adj_v = self.adjacent_set(v)
            for u, w_u_v in adj_v:
                if u not in S and distance[u] > distance[v] + w_u_v:
                    distance[u] = distance[v] + w_u_v
                    p[u] = v
                    pq.push((distance[u], u))

        sp = ShortestPath(s, distance, p)
        return sp

    def adjacent_set(self, v):
        adj_v = []
        for i in range(self.vertex_num):
            w = self.adj_matrix[v][i]
            if w:
                adj_v.append((i, w))
        return adj_v


if __name__ =="__main__":
    g = Graph(4)
    g.add_edge(0, 1, 10)
    g.add_edge(0, 2, 3)
    g.add_edge(1, 3, 5)
    g.add_edge(2, 1, 5)
    g.add_edge(2, 3, 8)
    g.add_edge(3, 1, 4)
    g.add_edge(3, 2, 12)
    source = 0
    sp = g.dijkstra(source)
    for i in range(g.vertex_num):
        print(f"distance[{i}] : {sp.distance[i]}, p[{i}] : {sp.p[i]}")
    dest = 3 
    print(f"path from {source} to {dest}")
    sp.print_shortest_path(dest)
    print() 

💭 음수 간선이 존재하게 될 경우 다익스트라 알고리즘을 사용하지 않는 이유

• (가중치의 합이 음수인) 음수 사이클의 발생 가능성

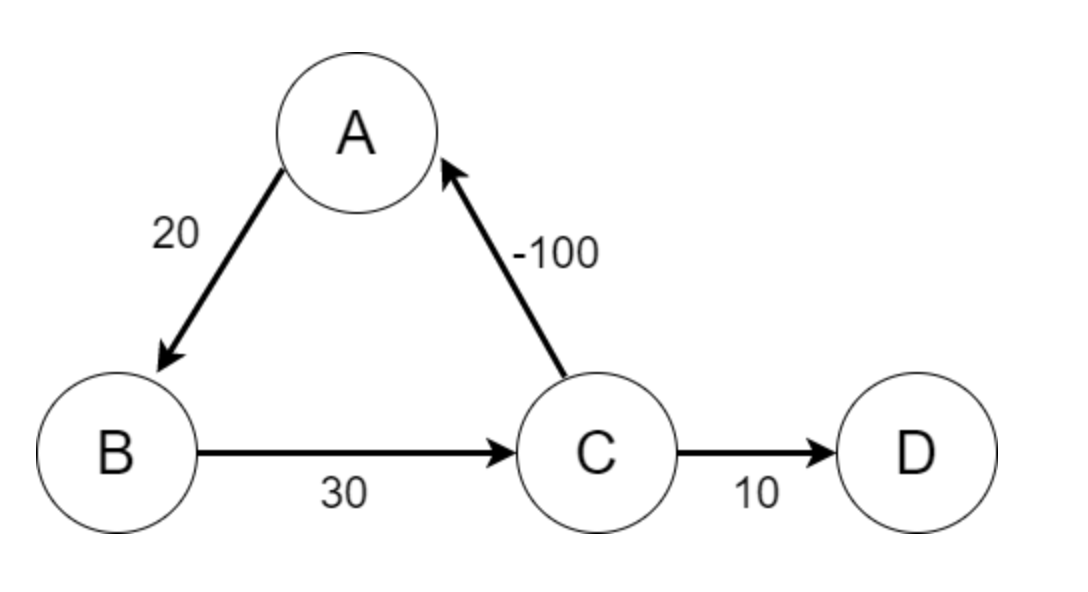
• 시작점을 A 라 할 때, A → D 까지 최단 경로는?
• A-B-C-D: 60
• A-B-C-A-B-C-D: 10
• A-B-C-A-B-C-A-B-C-D: -40

→ 가중치의 합이 음수인 사이클이 존재하게 되면 최단 경로가 음의 무한대로 발산하는 문제가 생깁니다.

• Edge Relaxation 계산의 오류 가능성

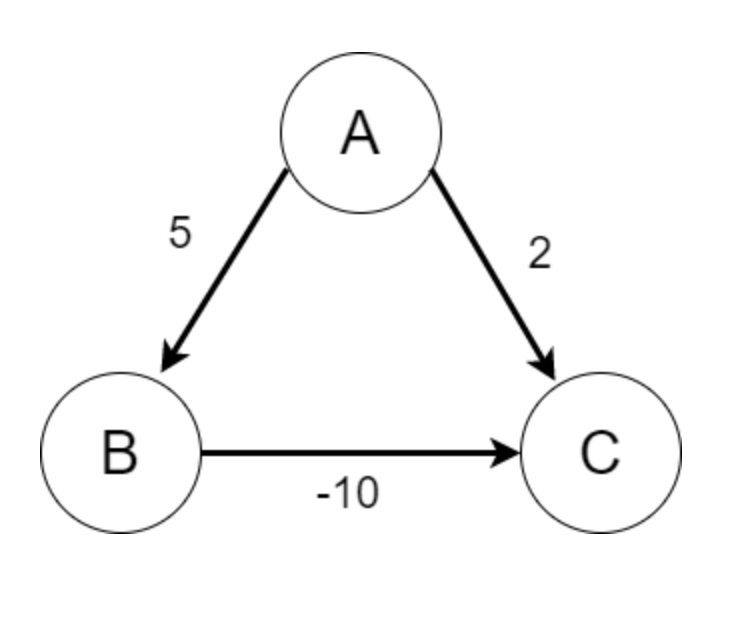
• min-heap 우선순위 큐를 사용하므로 초기 dist 값은 A를 제외하고 모두 양의 무한대
  • dist[A] + cost(A, C) < dist[C] 이기에 dist[C] 를 dist[A] + cost(A, C) 인 2 로 relax 연산을 해주고 dist[B] 도 마찬가지로 relax를 해줌
  • 이 후, A-C 의 가중치가 A-B 의 가중치보다 작기 때문에, pop 시 C 가 먼저 나오게 됨
  • 그리고 다익스트라 알고리즘은 C를 S 집합에 넣어주기 때문에 dist[C] 를 최단거리라 인식하고
    더이상 relax를 진행하지 않게됨

→ 따라서 dist[C] 는 2가 되지만 최단거리는 -5 이여야 하므로 알고리즘의 오류가 생기게 됩니다. 이는 다익스트라 알고리즘이 기본적으로 minimum 에 minimum 을 더하는 식으로 작동하기 때문입니다.

시작점이 minimum 이라는 원칙 아래에 인접노드들을 우선순위큐에 넣고, 가중치가 작은 것들부터 뽑아서 relax 를 하기 때문에 minimum + minimum = minimum 을 이용하여 최단거리를 찾기때문

Sources

• https://m.blog.naver.com/ndb796/221234424646
• https://mattlee.tistory.com/50
• https://hy38.github.io/why-dijkstra-fail-on-a-negative-weighted-edge